梯度下降(gradient descent)
定义代价函数(define a cost function)
平方代价函数(quadratic cost function)或均方误差(mean squared error or MSE)
\[C(w, b) = \frac{1}{2n}\sum_x\| y(x) - \hat{y}(x) \|^2 \tag{1}\label{eq1}\]其中,$w$ 代表网络中的全部权重值,$b$ 代表全部偏差值,$n$ 代表训练样本的总数,$\hat{y}(x)$ 是输入训练样本 $x$ 时网络的输出值,当然,$\hat{y}$ 同时依赖于 $w,b和x$,$y(x)$ 是训练样本 $x$ 对应的实际值。我们可以从平方代价函数看出两个特点:
- $C(w,b)$ 是一个非负数,因为它的每一项都是非负的。
- 当 $C(w,b)$ 变得越小,例如 $C(w,b)\approx 0$ 时,则输出值 $\hat{y}$ 越接近实际值 $y$。
所以,我们训练算法的目的就是找到合适的权重值($w$)和偏差值($b$),使得代价函数 $C(w,b)$ 尽可能的小。
为什么要引入平方代价函数呢?毕竟我们最初所感兴趣的内容是对图像正确地分类,那为什么不直接让输出值最大化接近实际的分类值,而是去间接最小化一个平方代价函数呢?这是因为在神经网络中,直接对权重和偏差做出改变有时并不会让输出值更接近实际值,这会导致我们很难去刻画如何优化权重和偏差才能得到更好的结果。而一个类似平方代价函数的函数能够指导我们如何去改变权重和偏差来达到更好的效果。这就是为何我们集中精力去最小化平方损失,只有通过这种方式我们才能让分类器更精确。
现在,我们可以集中精力处理如何最小化代价函数,我们将使用 梯度下降(gradient descent) 算法来最小化代价函数。
梯度的数学定义
方向导数 是函数 $z=f(x,y)$ 在点 $P(x,y)$ 处沿向量方向 $\boldsymbol l=\{\cos\alpha, \sin\alpha\}$ 上的方向导数,描绘了该点附近沿着该向量方向变动时的瞬时变化率。
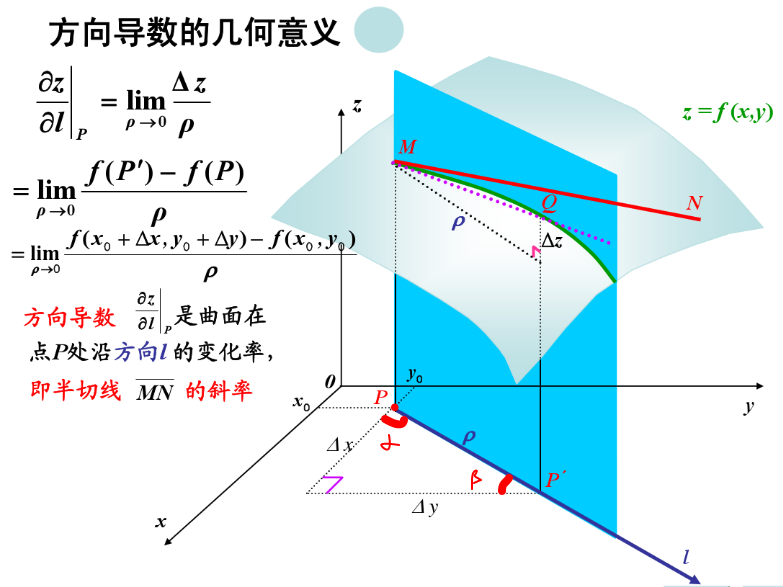
上图所示,函数在点 $P$ 沿着方向 $l$ 的 方向导数 表示为 $\frac{\partial{z}}{\partial{l}}|_P$,即沿着方向 $l$ 通过点 $P$ 的直线 $MN$ 对应函数曲面 $f$ 的斜率。计算方法是取 $P$ 点处于曲面函数的值 $f(P)$,然后在方向 $l$ 上取一个极小的距离 $\rho$ 得到点 $P’$,计算 $P’$ 点处函数的值 $f(P’)$,求得 $f(P’)-f(P)$ 的差值 $\Delta{z}$,然后将该差值除以 $\rho$,当 $\rho$ 趋近于 $0$ 时,得到的极限值就是该方向上的方向导数。
梯度 是函数 $f(x,y)$ 在点 $P(x,y)$ 处方向导数取得最大值的方向,是一个向量,梯度定义为:
\[\mathbf{grad}\,f = \nabla{f}=\frac{\partial{f}}{\partial{x}}\boldsymbol i+\frac{\partial{f}}{\partial{y}}\boldsymbol j = \left\{\frac{\partial{f}}{\partial{x}}, \frac{\partial{f}}{\partial{y}}\right\}\]最大的方向导数为梯度的模,即
\[|\mathbf{grad}\,f|=|\nabla{f}|=\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\]函数 $f(x,y)$ 在点 $M$ 处沿方向 $\boldsymbol l$ 的方向导数的计算等式为:
\[\frac{\partial f}{\partial l} = \nabla f \cdot \frac{\boldsymbol l}{|\boldsymbol l|} = \nabla f \cdot \boldsymbol l^0 = \frac{\partial f}{\partial x}\cos \alpha + \frac{\partial f}{\partial y}\cos \beta,其中\;\boldsymbol l^0=\{\cos \alpha, \cos \beta\}\]二元函数 $z=f(u,v), u=\varphi(x),v=\psi(x)$ 求导
\[f'(u,v)=\lim_{\substack{\Delta u \to 0 \\ \Delta v \to 0}} \frac{f(u+\Delta u, v+\Delta v)-f(u,v)}{\sqrt{(\Delta u)^2+(\Delta v)^2}}\] \[\frac{dz}{dx}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x}\]对于只有几个变量的函数,我们还有可能直接求出该函数的导数,但对于有很多个变量的函数来说,直接求导就太困难了,而神经网络通常都含有成千上万个变量。因此,对于神经网络,直接求导的方式根本不可行。
通过梯度下降学习参数
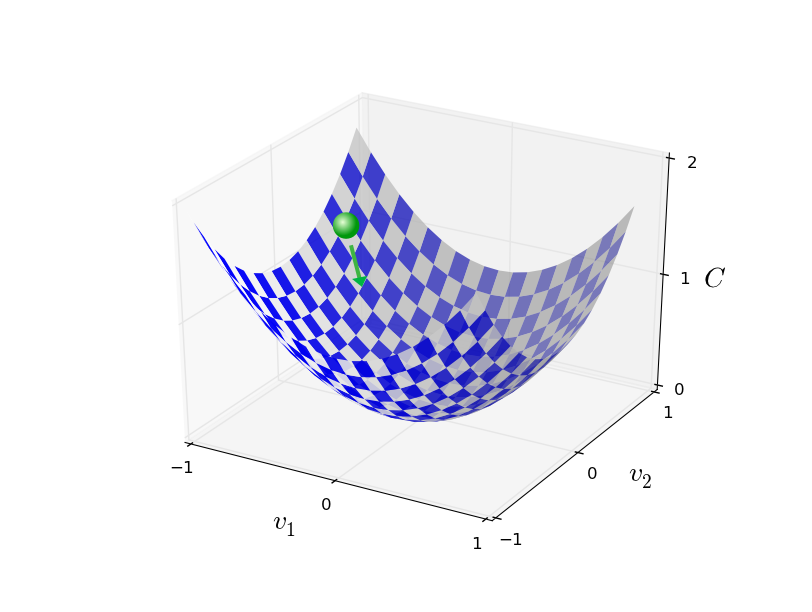
有一个不错的类比预示着有一种算法能得到很好的效果。首先把函数想象成一个山谷,然后想象有一个小球从山谷的斜坡滚落下来,日常经验告诉我们这个球终会达到谷底,也许我们可以用这种思路来找到函数最小值。我们随机地为小球选取一个起点,然后开始模拟小球滚落到谷底的运动过程。可以简单的通过计算 C 的导数(或者二阶导数)来模拟这个过程——这些导数将会告诉我们关于山谷「地形」的一切信息,从而告诉我们的小球该如何下落。
假如我们有一个只有两个变量的函数 $C(v_1,v_2)$,如果让小球在这个函数图形上移动一小点,即在 $v_1$ 方向移动 $\Delta v_1$,在 $v_2$ 方向移动 $\Delta v_2$,根据微分知识,我们知道小球大概移动了
\[\Delta C \approx \frac{\partial C}{\partial v_1}\Delta v_1 + \frac{\partial C}{\partial v_2}\Delta v_2 \tag{2}\label{eq2}\]我们把各方向上的微小改变量定义为一个向量:
\[\Delta\boldsymbol{v} = \begin{bmatrix} \Delta v_1 \\ \Delta v_2 \end{bmatrix}\]函数 $C$ 对于各个变量的偏导数也定义为一个向量,这个向量就是函数 $C$ 的梯度:
\[\nabla C=\begin{bmatrix} \frac{\partial C}{\partial v_1} \\ \frac{\partial C}{\partial v_2} \end{bmatrix}\]那么 $\Delta C$ 就可以改写为两个向量的点积:
\[\Delta C \approx \nabla C \cdot \Delta \boldsymbol{v} \tag{3}\label{eq3}\]如果我们选择
\[\Delta \boldsymbol{v} = -\eta \nabla C \tag{4}\label{eq4}\]那么 $\Delta C$ 就可以重写为:
\[\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta \|\nabla C\|^2 \tag{5}\label{eq5}\]由于 $\Vert\nabla C\Vert^2 \ge 0$,这就保证 $\Delta C \le 0$,当我们改变 $\boldsymbol{v}$ 时,$\Delta C$ 始终是个负值,因此 $C$ 就会一直减小。我们使用等式 \eqref{eq4} 计算出 $\boldsymbol{\Delta v}$,然后让小球从位置 $\boldsymbol{v}$ 移动 $\Delta \boldsymbol{v}$,
\[\boldsymbol{v} \to \boldsymbol{v'} = \boldsymbol{v} - \eta\nabla C \tag{6}\label{eq6}\]接着我们再次使用这个 更新规则(update_rule),让小球位置继续移动。 如果一直这样重复做下去,就会让代价函数$C$一直减小,直到达到我们希望的全局最小值。我们可以把等式 \eqref{eq6} 这个 更新规则(update_rule) 看作梯度下降的定义。
总结一下,梯度下降算法工作的方式就是重复计算梯度 $\nabla C$,然后沿着梯度的反方向运动,即沿着山谷的斜坡下降。
在神经网络里,我们通过梯度下降最小化等式 \eqref{eq1} 的平方代价函数,找到合适的权重$w_k$和偏差$b_l$。将权重和偏差替换掉上面等式\eqref{eq6}的变量$v$,那么
\[\nabla C_w = \begin{bmatrix} \frac{\partial C}{\partial w_0} \\ \frac{\partial C}{\partial w_1} \\ \vdots \\ \frac{\partial C}{\partial w_k} \end{bmatrix}\] \[\nabla C_b = \begin{bmatrix} \frac{\partial C}{\partial b_0} \\ \frac{\partial C}{\partial b_1} \\ \vdots \\ \frac{\partial C}{\partial b_l} \end{bmatrix}\]对应等式\eqref{eq6}的形式就是:
\[\begin{align} w_k \to w'_k &= w_k - \eta\nabla C \\ &= w_k - \eta\frac{\partial C}{\partial w_k} \tag{7}\label{eq7} \end{align}\] \[\begin{align} b_l \to b'_l &= b_l - \eta\nabla C \\ &= b_l - \eta\frac{\partial C}{\partial b_l} \tag{8}\label{eq8} \end{align}\]通过重复应用等式\eqref{eq7}和等式\eqref{eq8},我们就可以近似找到代价函数的最小值。
随机梯度下降
再回头看一下等式\eqref{eq1},注意到它其实是这样的一种形式 $C=\frac{1}{n}\sum_x C_x$,它是相对单个样本代价函数(也就是损失函数 loss function)$C_x=\frac{|y(x)-\hat{y}(x)|^2}{2}$ 的平均值。实际上,计算梯度 $\nabla C$ 需要计算每个训练样本的梯度 $\nabla C_x$ 然后求平均,$\nabla C=\frac{1}{n}\sum_x\nabla C_x$,如果训练样本集非常大的话,计算时间会非常长,学习将会很慢。
随机梯度下降(stochastic gradient descent)可以改善这种问题,它的思想是从训练集中随机选取一小部分样本,通过计算这一小部分样本的平均梯度 $\nabla C_x$ 来估计总体样本的平均梯度 $\nabla C$,这样就可以加快梯度下降,最终加快机器学习。
具体来讲,随机梯度下降从训练集中随机挑出 $m$ 个样本,我们把这些样本标记为 $x_1,x_2,\dots,x_m$,把他们叫做 mini-batch。它的数量 $m$ 应该足够大,这样它的平均梯度 $\nabla C_{x_m}$ 就应该非常接近总体样本的平均梯度 $\nabla C$
\[\frac{\sum_m\nabla C_{x_m}}{m} \approx \frac{\sum_x\nabla C_x}{n} = \nabla C \tag{9}\label{eq9}\]反过来写就是,
\[\nabla C \approx \frac{1}{m}\sum_m\nabla C_{x_m} \tag{10}\label{eq10}\]最终就是我们随机选择一个 mini-batch,通过计算它的平均梯度来估计总体的平均梯度。
与前面等式 \eqref{eq7} 和等式 \eqref{eq8} 里的权重 $w_k$ 和偏差 $b_l$ 联系起来,随机梯度下降通过从训练集随机选取一个 mini-batch 来训练权重和偏差,
\[\begin{align} w_k \to w'_k &= w_k - \frac{\eta}{m}\sum_m\nabla C_{x_m} \\ &= w_k - \frac{\eta}{m}\sum_m\frac{\partial C_{x_m}}{\partial w_k} \tag{11}\label{eq11} \end{align}\] \[\begin{align} b_l \to b'_l &= b_l - \frac{\eta}{m}\sum_m\nabla C_{x_m} \\ &= b_l - \frac{\eta}{m}\sum_m\frac{\partial C_{x_m}}{\partial b_l} \tag{12}\label{eq12} \end{align}\]我们对当前 mini-batch 中的所有训练样本 $x_m$ 通过求平均梯度 $\nabla C_{x_m}$ 进行训练,接着我们再随机挑选另一个 mini-batch 重复相同步骤,直到我们用完训练集中的所有样本,这样就完成了 一轮(epoch) 训练,然后我们开始新一轮的训练。
值得一提的是,通过缩放全体样本或 mini-batch 的代价函数来计算权重和偏差有很多不同的约定。在等式 \eqref{eq1} 中,我们通过因子 $\frac{1}{n}$ 来缩放代价函数,但有时也会忽略 $\frac{1}{n}$ ,直接计算单独训练样本损失之和,而不是求平均值,这在不能提前知道训练集大小的情况下特别有用,比如训练数据是实时产生的。同样,对于 mini-batch 的等式 \eqref{eq11} 和 \eqref{eq12} 有时也会舍弃求和前的 $\frac{1}{m}$ 。从概念上讲,这会有一点区别,因为它等于重新调节了学习速率 $\eta$ 。在对不同机器学习算法进行详细比较时,应该引起注意。
梯度下降一个极端版本就是让 mini-batch 的大小为 1。也就是说,一次只给一个训练样本 $x$,通过规则 $w_k \to w’_k = w_k−\eta\frac{\partial C_x}{\partial w_k}$ 和 $b_l \to b’_l = b_l-\eta\frac{\partial C_x}{\partial b_l}$ 更新权重和偏差,接着选择下一个训练样本再次更新权重和偏差,一直这样重复下去,这种处理方式就是 在线学习(online learning) 或 增量学习(incremental learning)。在在线学习中,神经网络一次只学习一个训练数据(就像我们人类做的那样)。
反向传播 (back propagation)
前向传播 (forward propagation)
下面给出神经网络中权重、偏差和激活值的明确定义
-
$w^l_{jk}$ 表示连接从第 $(l-1)$ 层的第 $k$ 神经元到第 $l$ 层的第 $j$ 个神经元的权重
-
$b^l_j$ 表示第 $l$ 层的第 $j$ 个神经元的偏差
-
$a^l_j$ 表示第 $l$ 层的第 $j$ 个神经元的激活值
那么第 $l$ 层的第 $j$ 个神经元的激活值 $a^l_j$ 可以表示为
\[a^{(1)}_0 = \sigma\left( \begin{bmatrix} w^{(1)}_{00} & w^{(1)}_{01} & \ldots & w^{(1)}_{0n} \end{bmatrix} \begin{bmatrix} a^{(0)}_0 \\ a^{(0)}_1 \\ \vdots \\ a^{(0)}_n \end{bmatrix} + b^{(1)}_0 \right)\]即:
\[a^l_j = \sigma\left(\sum_k w^l_{jk}a^{l-1}_k + b^l_j\right) \tag{13}\label{eq13}\]将等式 \eqref{eq13} 改写为 矩阵-向量 形式,$w^l$ 表示第 $l$ 层的 权重矩阵,$b^l$ 表示第 $l$ 层的 偏差向量,$a^l$ 表示第 $l$ 层的 激活值向量,最后激活函数 $\sigma$ 也支持向量化,即对向量 $v$ 应用函数 $\sigma$ 相当于对向量 $v$ 中的每个分量分别应用函数 $\sigma$。
\[\begin{bmatrix} a^{(1)}_0 \\ a^{(1)}_1 \\ \vdots \\ a^{(1)}_m \end{bmatrix} = \sigma\left( \begin{bmatrix} w^{(1)}_{00} & w^{(1)}_{01} & \ldots & w^{(1)}_{0n} \\ w^{(1)}_{10} & w^{(1)}_{11} & \ldots & w^{(1)}_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ w^{(1)}_{m0} & w^{(1)}_{m1} & \ldots & w^{(1)}_{mn} \end{bmatrix} \begin{bmatrix} a^{(0)}_0 \\ a^{(0)}_1 \\ \vdots \\ a^{(0)}_n \end{bmatrix} + \begin{bmatrix} b^{(1)}_0 \\ b^{(1)}_1 \\ \vdots \\ b^{(1)}_m \end{bmatrix} \right)\]即:
\[a^l = \sigma(w^la^{l-1} + b^l) \tag{14}\label{eq14}\]
另外,把等式 \eqref{eq14} 的中间形式定义为
\[z^l \equiv w^la^{l-1} + b^l\]把 $z^l$ 叫做第 $l$ 层神经元的 加权输入(weighted input),所以有时候等式 \eqref{eq14} 写成 $a^l=\sigma(z^l)$,同时它的非向量化形式为 $a^l_j=\sum_k w^l_{jk}a^{l-1}_k + b^l_j$
代价函数的两个假设
反向传播的目的就是求代价函数 $C$ 关于神经网络中权重和偏差的偏导数 $\frac{\partial C}{\partial w}$ 和 $\frac{\partial C}{\partial b}$,要使用反向传播,代价函数 $C$ 必须满足两个主要假设,我们使用等式 \eqref{eq1} 中的平方代价函数为例,
\[C(w, b) = \frac{1}{2n}\sum_x\| y(x) - a^L(x) \|^2 \tag{15}\label{eq15}\]其中,$n$ 代表训练样本的总数,求和是针对所有训练样本 $x$,$y=y(x)$ 是对应的期望值,$L$ 表示网络中的层数,$a^L=a^L(x)$ 是当输入样本 $x$ 后神经网络的输出向量。
第一个假设是,代价函数 $C$ 可以写为对所有训练样本 $x$ 的代价函数 $C_x$ 求平均值 $C=\frac{1}{n}\sum_xC_x$,原因是反向传播实际上是计算的单个训练样本的权重和偏差的偏导数 $\frac{\partial C_x}{\partial w}$ 和 $\frac{\partial C_x}{\partial b}$,然后对所有训练样本的权重和偏差偏导数求平均 $\frac{\partial C}{\partial w}$ 和 $\frac{\partial C}{\partial b}$,拿平方代价函数来说,单个训练样本的代价函数就是 $C_x=\frac{1}{2}\Vert y-a^L \Vert^2$ (损失函数,loss function)。
第二个假设是,代价函数 $C$ 可以写为关于神经网络输出值的函数 $C=C(a^L(x))$。
哈达玛积 (Hadamard product) $s \odot t$
Hadamard product 是指两个相同维度的矩阵或向量,它们的 对应元素(elementwise) 相乘。因此,同维向量 $s$ 和 $t$ 的 Hadamard 积写作$(s \odot t)_j=s_jt_j$,
\[\begin{bmatrix} 1 \\ 2 \end{bmatrix} \odot \begin{bmatrix} 3 \\ 4 \end{bmatrix} =\begin{bmatrix} 1*3 \\ 2*4 \end{bmatrix} =\begin{bmatrix} 3 \\ 8 \end{bmatrix}\]同维矩阵 $A$ 和 $B$ 的 Hadamard 积写作
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \odot \begin{bmatrix} 2 & 0 \\ 1 & 3 \end{bmatrix} =\begin{bmatrix} 1*2 & 2*0 \\ 3*1 & 4*3 \end{bmatrix} =\begin{bmatrix} 2 & 0 \\ 3 & 12 \end{bmatrix}\]反向传播的四个基本等式
首先定义第 $l$ 层第 $j$ 个神经元对应的错误量 $\delta^l_j$ 为,
\[\delta^l_j \equiv \frac{\partial C}{\partial z^l_j} \tag{16}\label{eq16}\]输出层中关于错误量 $\delta^L$ 的等式
\[\delta^L_j = \frac{\partial C}{\partial a^L_j}\sigma'(z^L_j) \tag{BP1}\label{BP1}\]$\frac{\partial C}{\partial a^L_j}$ 用于度量代价函数 $C$ 对于第 $j$ 个输出激活值的变化率。因此,如果 $C$ 不太依赖第 $j$ 个神经元,那么 $\delta^L_j$ 就应当很小,这也是我们期望的。 $\sigma’(z^L_j)$ 度量激活函数 $\sigma$ 对于 $z^L_j$ 的变化率。$\frac{\partial C}{\partial a^L_j}$ 的具体形式依赖于使用的代价函数,如果使用平方代价函数,则 $C=\frac{1}{2}\sum_j(y_j-a^L_j)^2$,那么 $\frac{\partial C}{\partial a^L_j}=(a^L_j-y_j)$。
$\delta^L_j$ 是 $\delta^L$ 的分量化表达形式,其矩阵-向量形式为
\[\delta^L = \nabla_a C \odot \sigma'(z^L) \tag{BP1a}\label{BP1a}\]$\nabla_a C$ 定义为一个向量,其分量是输出层各神经元的偏导数 $\frac{\partial C}{\partial a^L_j}$,对于平方代价函数,$\nabla_a C=(a^L-y)$,其使用等式 \eqref{BP1} 的完整矩阵-向量形式为:
\[\delta^L = (a^L-y) \odot \sigma'(z^L) \tag{17}\label{eq17}\]根据错误量 $\delta^{l+1}$ 得到错误量 $\delta^l$ 的等式
\[\delta^l = ((w^{l+1})^T\delta^{l+1}) \odot \sigma'(z^l) \tag{BP2}\label{BP2}\]$(w^{l+1})^T$ 是第 $(l+1)$ 层的权重矩阵 $w^{l+1}$ 的转置。该等式含义是,假如我们知道第 $(l+1)$ 层的错误量 $\delta^{l+1}$,通过对其应用权重矩阵的转置 $(w^{l+1})^T$,可以直观理解为错误量在神经网络里 反向 移动了,这给了我们计算第 $l$ 层错误量的方法,再与 $\sigma’(z^l)$ 应用 Hadamard 积,将错误量通过第 $l$ 层的激活函数反向移动,得到第 $l$ 层加权输入的错误量 $\delta^l$
通过 \eqref{BP1} 和 \eqref{BP2} 我们可以计算神经网络中任意层的错误量 $\delta^l$。我们先计算输出层的错误量 $\delta^L$,然后使用等式 \eqref{BP2} 计算 $\delta^{L-1}$,然后再使用等式 \eqref{BP2} 计算 $\delta^{L-2}$,以此类推,就可以反向穿过整个神经网络。
神经网络中代价函数关于任一偏差的变化率的等式
\[\frac{\partial C}{\partial b^l_j} = \delta^l_j \tag{BP3}\label{BP3}\]也就是说,错误量 $\delta^l_j$ 完全等于变化率 $\frac{\partial C}{\partial b^l_j}$。写成向量形式就是,
\[\frac{\partial C}{\partial b} = \delta \tag{18}\label{eq18}\]神经网络中代价函数关于任一权重的变化率的等式
\[\frac{\partial C}{\partial w^l_{jk}} = \delta^l_ja^{l-1}_k \tag{BP4}\label{BP4}\]这告诉我们如何通过 $\delta^l$ 和 $a^{l-1}$ 来计算 $\frac{\partial C}{\partial w^l_{jk}}$,等式可以重写为无下标的形式,
\[\frac{\partial C}{\partial w} = a_{in}\delta_{out} \tag{19}\label{eq19}\]其中,$a_{in}$ 是输入到权重 $w$ 的激活神经元,$\delta_{out}$ 是从权重 $w$ 输出的神经元的错误量。等式 \eqref{eq19} 有个很好的结论是,当 $a_{in}$ 很小时,$a_{in} \approx 0$,梯度 $\frac{\partial C}{\partial w}$ 也会变得很小,这种情况下,可以说 权重学习的很慢,这意味着梯度没有多大改变。换句话说,\eqref{BP4} 说明,从一个低激活值神经元连接出来的权重,会学习的很慢。
通过 \eqref{BP1} - \eqref{BP4} 我们可以更深入的理解机器学习。从输出层开始,考虑 \eqref{BP1} 的 $\sigma’(z^L_j)$ 项,根据激活函数 sigmoid 的图像特点,当 $\sigma(z^L_j)$ 接近 0 或 1 的时候它会变得非常平缓,这会让它的导数 $\sigma’(z^L_j) \approx 0$,所以当输出层神经元 $a^L_j$ 是低激活值 $(\approx 0)$ 或高激活值 $(\approx 1)$ 时,输出层的权重都会学习的很慢,这种情况下,通常可以说输出层的神经元已经 饱和(saturated) 了,结果就是权重停止学习或学习很慢。
输出层之前的网络层也有相似的结论,注意到 \eqref{BP2} 中的 $\sigma’(z^l_j)$,这意味着当神经元已经接近饱和的时候 $\delta^l_j$ 很可能会变小,也就是任何输入到饱和神经元的权重,学习都会变得缓慢。
总结起来就是,不管输入神经元是低激活值的,还是输出神经元是饱和的(高激活值或低激活值),权重的学习都会变得缓慢。

反向传播等式的证明
首先是等式 \eqref{BP1},直接应用链式求导法则
\[\begin{align} \delta^L_j &= \frac{\partial C}{\partial z^L_j} \\ &= \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j} \\ &= \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j} \\ &= \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \tag{20}\label{eq20} \end{align}\]然后证明等式 \eqref{BP2}
\[\begin{align} \delta^l_j &= \frac{\partial C}{\partial z^l_j} \\ &= \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \\ &= \sum_k \delta^{l+1}_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{21}\label{eq21} \end{align}\]其中
\[z^{l+1}_k = \sum_j w^{l+1}_{kj} a^l_j +b^{l+1}_k = \sum_j w^{l+1}_{kj} \sigma(z^l_j) +b^{l+1}_k \tag{22}\label{eq22}\]上式对 $z^l_j$ 求导后得到
\[\frac{\partial z^{l+1}_k}{\partial z^l_j} = w^{l+1}_{kj} \sigma'(z^l_j) \tag{23}\label{eq23}\]代入到 \eqref{eq21} 后得到
\[\delta^l_j = \sum_k \delta^{l+1}_k w^{l+1}_{kj} \sigma'(z^l_j) \tag{24}\label{eq24}\]反向传播算法
反射传播等式给了我们计算代价函数梯度的方法,
-
输入 (Input)
$x$: 设置输入层对应的激活值 $a^1$
-
前向传播 (FeedForward)
对每一层 $l=2,3,…,L$ 计算 $z^l = w^la^{l-1} + b^l$ 和 $a^l = \sigma(z^l)$
-
输出的错误量 (Output error)
计算向量 $\delta^L = \nabla_a C \odot \sigma’(z)$
-
将错误量反向传播 (Backpropagate the error)
对每一层 $l=L-1, L-2,…,2$ 计算 $\delta^l = ((w^{l+1})^T\delta^{l+1}) \odot \sigma’(z^l)$
-
输出 (Output)
代价函数关于权重和偏差的梯度为 $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k\delta^l_j$ 和 $\frac{\partial C}{\partial b^l_j} = \delta^l_j$