基本概念
假设函数 (Hypothesis Function): 根据输入的特征来预测输出结果。它是从输入变量到输出变量的函数,从输入特征空间到输出标签空间的映射,通常表示为 $h_\theta(x)$。在有监督学习中,这个函数通常是由训练数据中学习得到的,这就是为什么要叫 机器学习,所有训练出来的权重参数,都是用来逼进这个函数,我们希望通过这个学习出来的假设函数,可以从新的数据预测出想要的结果。
损失函数 (Loss Function):描述的是单个训练样本的预测值与真实值之间的误差。损失函数是关于单一训练样本的函数,它度量了一个样本的预测值与实际值的差异。例如,在回归任务中常用的损失函数是平方损失函数 $L(\theta)=(h_\theta(x)-y)^2$,其中是 $h_\theta(x)$ 预测值, $y$ 是真实值。
线性回归(Linear Regression)
假设函数(Hypothesis Function): 线性函数
\[h_\theta(x) = \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n + b = [\theta_1 \ \theta_2 \ \dots \ \theta_n] \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} + b = \theta^Tx+b \text{ (单个样本)}\] \[h_\theta(x) = \begin{bmatrix} h_\theta(x^{(1)}) \\ h_\theta(x^{(2)}) \\ \vdots \\ h_\theta(x^{(m)}) \end{bmatrix} = \begin{bmatrix} \theta_1x^{(1)}_1 + \theta_2x^{(1)}_2 + \dots + \theta_nx^{(1)}_n + b \\ \theta_1x^{(2)}_1 + \theta_2x^{(2)}_2 + \dots + \theta_nx^{(2)}_n + b \\ \vdots \\ \theta_1x^{(m)}_1 + \theta_2x^{(m)}_2 + \dots + \theta_nx^{(m)}_n + b \\ \end{bmatrix} = \begin{bmatrix} x^{(1)}_1 \ x^{(1)}_2 \ \dots \ x^{(1)}_n \\ x^{(2)}_1 \ x^{(2)}_2 \ \dots \ x^{(2)}_n \\ \vdots \\ x^{(m)}_1 \ x^{(m)}_2 \ \dots \ x^{(m)}_n \\ \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{bmatrix} + \begin{bmatrix} b \\ b \\ \vdots \\ b \end{bmatrix} = X\theta + b \text{ (多个样本)}\]代价函数:
\[\begin{align} Loss &= \frac{1}{2}(h_\theta(x) - y)^2 \\ &= \frac{1}{2}(\theta^Tx - y)^2 \text{ (单个样本)} \end{align}\] \[\begin{align} J(\theta) &= \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 \\ &= \frac{1}{2m}(X\theta - y)^T(X\theta - y) \text{ (多个样本)} \end{align}\]需要注意,多样本代价函数是所有样本全部参与计算,得出一个总体代价值。
代价函数关于 $\theta_j$ 的导数:
\[\begin{align} \frac{\partial}{\partial\theta_j}J(\theta) &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j \\ &= \frac{1}{m}x_j^T(X\theta - y) \text{ (单个参数)} \end{align}\] \[\begin{align} \frac{\partial}{\partial\theta}J(\theta) &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)} \\ &= \frac{1}{m}X^T(X\theta - y) \text{ (所有参数)} \end{align}\]梯度下降:
\[\begin{align} \theta_j &= \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta) \\ &= \theta_j - \frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j \\ &= \theta_j - \frac{\alpha}{m}x_j^T(X\theta - y) \end{align}\]$\alpha$ 表示学习率(learning rate),$\alpha$ 越大,梯度下降越快,但 $\alpha$ 过大会导致代价函数无法收敛。
向量形式:
\[\theta = \theta - \frac{\alpha}{m}X^T(X\theta - y)\]逻辑回归(Logistic Regression)
假设函数: 逻辑函数(Logistic Function 或 Sigmoid Function)
\[z = \theta^Tx \text{ (单个样本)} \\ z = X\theta \text{ (多个样本)}\] \[h_\theta(x) = g(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^Tx}} \text{ (单个样本)} \\ h_\theta(x) = g(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-X\theta}} \text{ (多个样本)} \\\]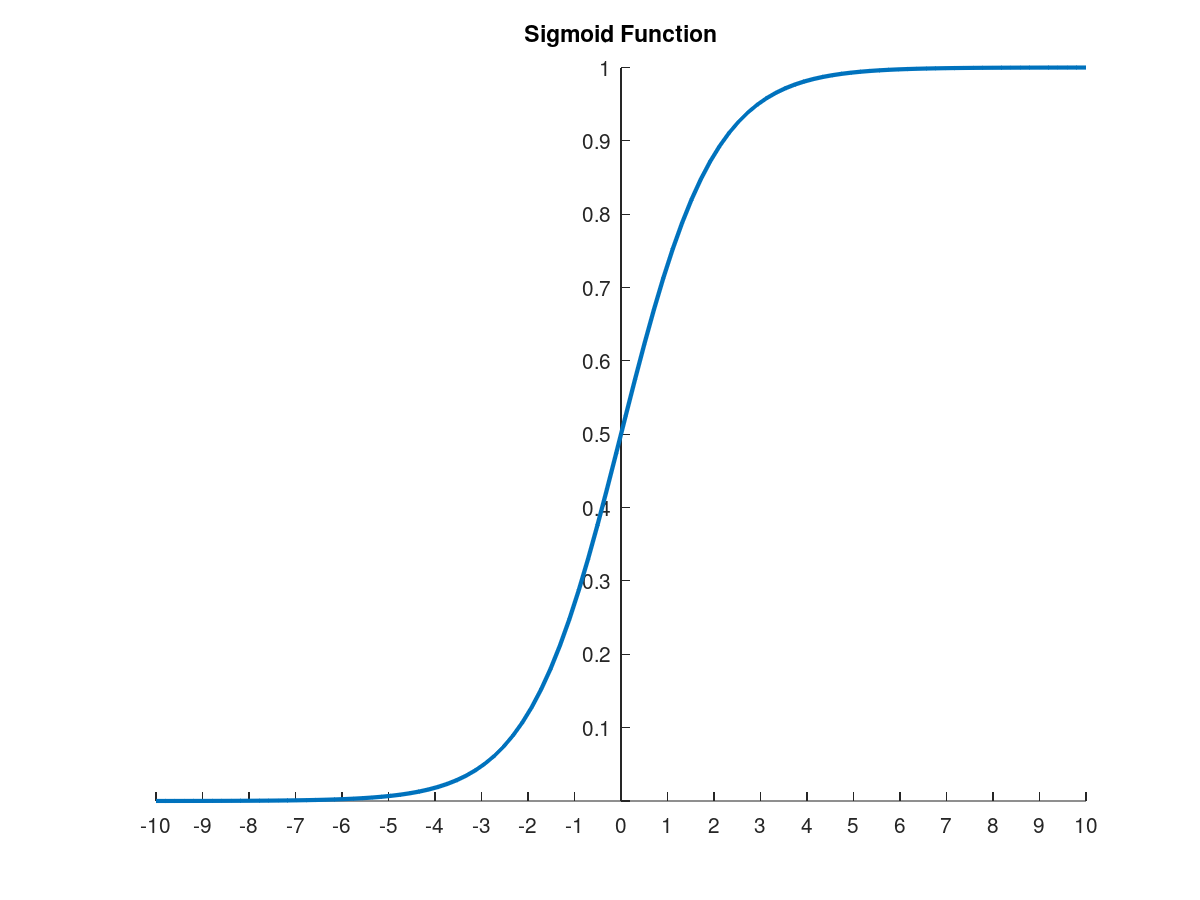
代价函数:
\[Loss = \begin{cases} -\log(h_\theta(x)) & \text{if } y = 1 \\ -\log(1 - h_\theta(x)) & \text{if } y = 0 \end{cases}\]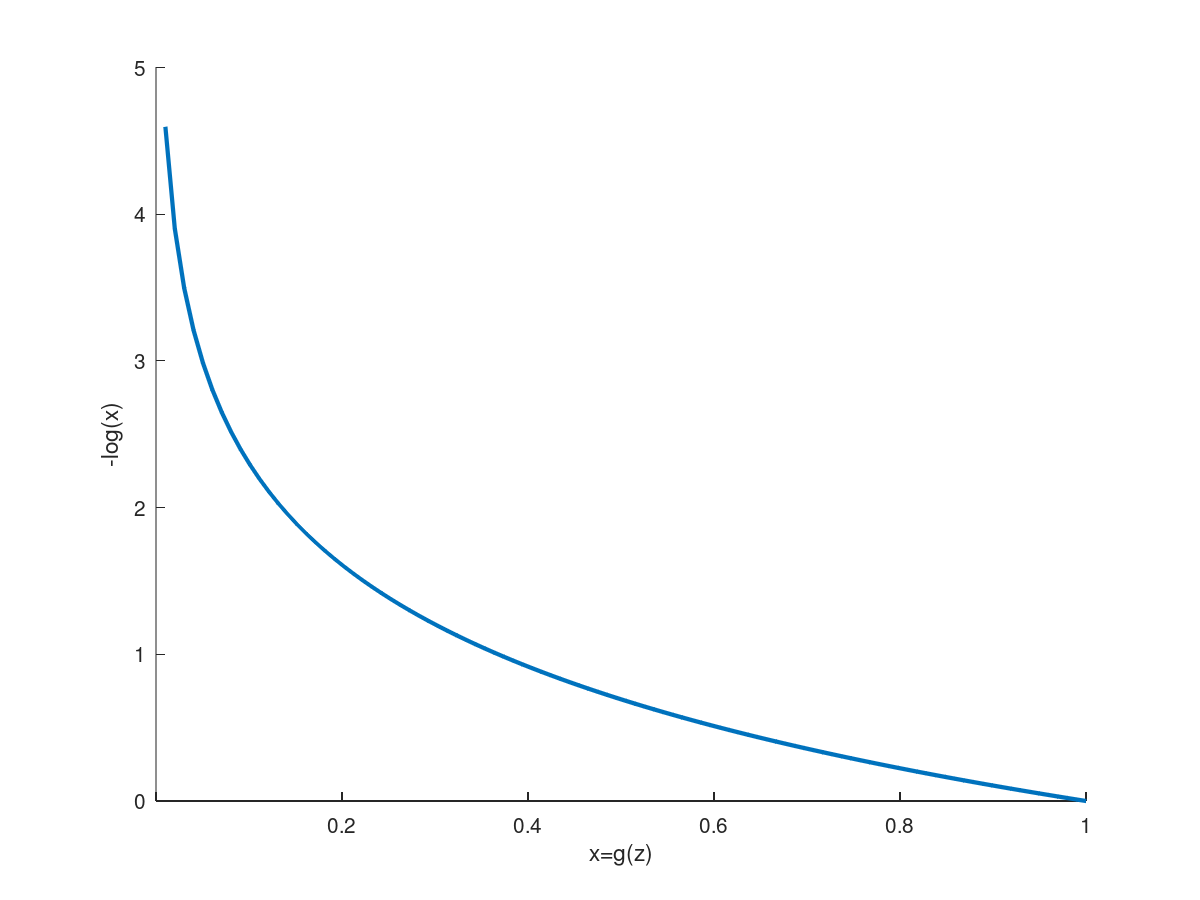
代价函数的单行形式:
\[\begin{align} Loss &= -y\log(h_\theta(x)) - (1-y)\log(1-h_\theta(x)) \\ &= -y\log(g(\theta^Tx)) - (1-y)\log(1-g(\theta^Tx)) \text{ (单个样本)} \end{align}\] \[\begin{align} J(\theta) &= \frac{1}{m}\sum_{i=1}^m[-y^{(i)}\log(h_\theta(x^{(i)})) - (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] \\ &= \frac{1}{m}(-y^T\log(g(X\theta)) - (1-y^T)\log(1-g(X\theta))) \text{ (多个样本)} \end{align}\]代价函数关于 $\theta_j$ 的导数(与线性回归相似,但 $h_\theta(x) = g(X\theta)$):
\[\begin{align} \frac{\partial}{\partial\theta_j}J(\theta) &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j \\ &= \frac{1}{m}x_j^T(g(X\theta) - y) \text{ (单个参数)} \end{align}\] \[\begin{align} \frac{\partial}{\partial\theta}J(\theta) &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)} \\ &= \frac{1}{m}X^T(g(X\theta) - y) \text{ (所有参数)} \end{align}\]梯度下降:
\[\begin{align} \theta_j &= \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta) \\ &= \theta_j - \frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j \\ &= \theta_j - \frac{\alpha}{m}x_j^T(g(X\theta) - y) \end{align}\]向量形式:
\[\theta = \theta - \frac{\alpha}{m}X^T(g(X\theta) - y)\]正则化(Regularization)
为了防止假设函数过拟合,可以减小参数 $\theta$ 来对相应的特征进行惩罚,方法是给代价函数添加正则化项 $\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$。需要注意,正则化不包括 $\theta_0$ (即偏差项)。
\[\begin{align} J_{reg}(\theta) &= J(\theta) + \color{red}{\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2} \\ &= J(\theta) + \color{red}{\frac{\lambda}{2m}\theta^T\theta} \end{align}\]$\lambda$ 表示正则化参数(regularization parameter),$\lambda$ 越大,假设函数越平缓,但 $\lambda$ 过大会导致假设函数欠拟合。
正则化后的线性回归代价函数:
\[J_{reg}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \color{red}{\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2} \\\]正则化后的逻辑回归代价函数:
\[J_{reg}(\theta) = \frac{1}{m}\sum_{i=1}^m[-y^{(i)}\log(h_\theta(x^{(i)})) - (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] + \color{red}{\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2}\]正则化后的代价函数关于 $\theta_j$ 的导数:
\[\frac{\partial}{\partial\theta_j}J_{reg}(\theta) = \frac{\partial}{\partial\theta_j}J(\theta) + \color{red}{\frac{\lambda}{m}\theta_j} \text{ (单个参数)}\] \[\frac{\partial}{\partial\theta}J_{reg}(\theta) = \frac{\partial}{\partial\theta}J(\theta) + \color{red}{\frac{\lambda}{m}\theta} \text{ (所有参数)}\]正则化后的梯度下降:
\[\begin{cases} \theta_0 &= \theta_0 - \alpha\dfrac{\partial}{\partial\theta_0}J(\theta) & \text{(不对} \theta_0 \text{进行正则化)} \\ \theta_j &= \theta_j - \alpha\left[\dfrac{\partial}{\partial\theta_j}J(\theta) + \color{red}{\dfrac{\lambda}{m}\theta_j}\right] \\ &= (1-\color{red}{\alpha\dfrac{\lambda}{m}})\theta_j - \alpha\dfrac{\partial}{\partial\theta_j}J(\theta) & (j = 1, 2, \dots, n) \end{cases}\]计算正则化梯度的一种向量化方法:
\[\theta = \theta - \alpha\left[\dfrac{\partial}{\partial\theta}J(\theta) + \dfrac{\lambda}{m}\color{red}{\tilde{\theta}}\right]\]其中
\[\theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix} \qquad \color{red}{\tilde{\theta}} = \begin{bmatrix} \color{red}{0} \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}\]