线性代数 (Linear Algebra)

一、线性方程组

行初等变换

1. 倍加变换：把某一行的倍数加到另一行上。
2. 对换变换：把两行对换。
3. 倍乘变换：把某一行的所有元素乘以同一个非零数。

线性方程组

\[\begin{aligned} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2 \\ \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m \end{aligned}\]

它的系数矩阵

\[\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\]

它的增广矩阵

\[\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{bmatrix}\]

把每列记作向量 $\mathbf{a}_i$，即

\[\mathbf{[a_1 \quad a_2 \quad \cdots \quad a_n \quad b]}\]

它的向量方程

\[x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n = \mathbf{b}\]

它的张成空间

\[\mathbf{Span}\{\mathbf{a_1, a_2, \cdots, a_n}\}\]

它的矩阵方程

\[A\mathbf{x} = [\mathbf{a_1 a_2 \cdots a_n}] \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n\]

由 $\mathbb{R}^n$ 到 $\Bbb R^m$ 的一个变换(或称函数、映射) $T$ 记为 $\Bbb R^n \to \Bbb R^m$。对 $\Bbb R^n$ 中的每个 $x$，$T(x)$ 由 $A(x)$ 计算得到，对应的矩阵变换记为 $x \to Ax$。矩阵 $A$ 也称为线性变换 $T$ 的标准矩阵。

1.3 向量方程

线性组合张成的集合

线性代数一个主要思想是研究可以表示为某一 固定向量集合 $\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 的线性组合的所有向量。

定义 $\quad$ 若 $\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 是 $\Bbb R^n$ 中的向量，则 $\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 的所有线性组合所成的集合用记号 $\mathbf{Span}\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 表示，称为由 $\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 生成(或张成)的 $\Bbb R^n$ 子集。也就是说，$\mathbf{Span}\{\mathbf{v_1,v_2,\cdots,v_p}\}$ 是所有 \(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + \cdots + c_p\mathbf{v}_p\)

所表示的向量的集合，其中 $c_1,c_2,\cdots,c_p$ 为标量。即,

\[\mathbf{Span}\{\mathbf{v_1,v_2,\cdots,v_p}\} = \{c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + \cdots + c_p\mathbf{v}_p\}\]

存在性与惟一性

线性方程组

• 是相容的，则它有一个或无穷多个解；

• 是不相容的，则它无解。

相容	相容	不相容
惟一解	无穷解	无解
没有自由变量 (线性无关)	有自由变量 (线性相关)
系数矩阵 $A$ 在每一行都有主元位置		增广矩阵最右列存在主元，即存在如下形式 $\mathbf{[0 \cdots 0 \; b] \; (b\ne0)}$
		$\mathbf b$ 不属于 $\mathbf{Span}\{\mathbf{a_1, a_2, \cdots, a_n\}}$
齐次方程 $Ax=0$ 仅有平凡解	齐次方程 $Ax=0$ 有非平凡解	方程 $Ax$ 无解
映射 $T: \Bbb R^n \to \Bbb R^m$ 是单射(一对一)	映射 $T: \Bbb R^n \to \Bbb R^m$ 是满射但不是单射	映射 $T$ 没有将 $\Bbb R^n$ 映射到 $\Bbb R^m$ 上

自由变量，矩阵的列数量大于行数量

线性无关

$\Bbb R^m$ 中的一组向量$\mathbf{\{a_1,\cdots,a_n\}}$ 称为

• 线性无关 $\quad$ 若向量方程 \(x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n = \mathbf{0}\) 只有 $\mathbf{x=0}$ ($\Bbb R^m$ 中的零向量) 这一个解(平凡解)，则称这组向量是线性无关的。

• 线性相关 $\quad$ 若存在不全为零的权 $x_1,\cdots,x_n$，使 \(x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n = \mathbf{0}\) 即至少有一个向量是其它向量的线性组合 \(x_1\mathbf{a}_1 + x_2\mathbf{a}_2 + \cdots + x_{n-1}\mathbf{a}_{n-1} = x_j\mathbf{a}_j\) 也就是说向量 $\mathbf a_j$ 落在了其它向量张成的空间中。

矩阵 $A$ 的各列线性无关，当且仅当方程 $A\mathbf x=\mathbf 0$ 仅有平凡解。

两个向量的集合 $\{v_1,v_2\}$ 线性相关，当且仅当其中一个向量是另一个向量的倍数。

若一个向量组的向量个数超过每个向量的元素个数时，这个向量组线性相关。也就是说 $\Bbb R^m$ 中的任意向量组 $\mathbf{\{a_1,\cdots,a_n\}}$，当 $n \gt m$ 时线性相关。

若向量组中包括 $\mathbf{\{a_1,\cdots,a_n\}}$ 零向量，则它线性相关。

1.8 线性变换介绍

由 $\Bbb R^n$ 到 $\Bbb R^m$ 的一个变换 (或称函数、映射) $T$ 是一个规则，它把 $\Bbb R^n$ 中的每个向量 $\mathbf{x}$ 对应以 $\Bbb R^m$ 中的一个向量 $T(\mathbf{x})$. 集 $\Bbb R^n$ 称为 $T$ 的定义域，而 $\Bbb R^m$ 称为 $T$ 的余定义域 (或取值空间). 符号 $T: \Bbb R^n \to \Bbb R^m$ 说明 $T$ 的定义域是 $\Bbb R^n$ 而余定义域是 $\Bbb R^m$，对于 $\Bbb R^n$ 中的向量 $\mathbf{x}$，$\Bbb R^m$ 中的向量 $T(\mathbf{x})$ 称为 $\mathbf{x}$ (在 $T$ 作用下) 的像. 所有像 $T(\mathbf{x})$ 的集合称为 $T$ 的值域.

定义 $\quad$ 变换 (或映射) $T$ 是线性的，若

1. 对 $T$ 的定义域中一切 $\mathbf{u,v},T(\mathbf{u+v})=T(\mathbf{u})+T(\mathbf{v})$.
2. 对一切 $\mathbf{u}$ 和标量 $c,T(c\mathbf{u})=cT(\mathbf{u})$.

每个矩阵变换都是线性变换.

1.9 线性变换的矩阵

定理 10 $\quad$ 设 $T:\Bbb R^n \to \Bbb R^m$ 为线性变换，则存在惟一的矩阵 $A$，使

\[T(\mathbf{x}) = A\mathbf{x}，对 \Bbb R^n 中的一切 \mathbf{x}\]

事实上，$A$ 是 $m \times n$ 矩阵，它的第 $j$ 列是向量 $T(\mathbf{e}_j)$，其中 $\mathbf{e}_j$ 是单位矩阵 $I_n$ 的第 $j$ 列:

\[A = [T(\mathbf{e}_1) \quad \cdots \quad T(\mathbf{e}_n)] \tag{1.3}\label{eq1.3}\]

\eqref{eq1.3} 中矩阵 $A$ 称为线性变换 $T$ 的标准矩阵.

术语线性变换强调映射的性质，而矩阵变换描述这样的映射如何实现.

二、矩阵代数

2.1 矩阵运算

矩阵转置

\[(AB \cdots N)^T = N^T \cdots B^T A^T\]

2.2 矩阵的逆

初等矩阵

把单位矩阵进行一次行变换，就得到初等矩阵。

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \xrightarrow{\text{倍加变换}} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -3 & 0 & 1 \end{bmatrix} \qquad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \xrightarrow{\text{对换变换}} \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \qquad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \xrightarrow{\text{倍乘变换}} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 5 \end{bmatrix}\]

若对 $m \times n$ 矩阵 $A$ 进行某种初等行变换，所得矩阵可以写成 $EA$，其中 $E$ 是 $m \times m$ 矩阵，是由 $I_m$ 进行同一行变换所得。

定理 7 $\quad$ 若 $n \times n$ 矩阵 $A$ 可逆，当且仅当 $A$ 行等价于 $I_n$，这时，把 $A$ 变成 $I_n$ 的一系列初等行变换同时把 $I_n$ 变为 $A^{-1}$。于是，

\[AA^{-1} = I \quad 且 \quad A^{-1}A = I\]

若 $A$ 是可逆 $n \times n$ 矩阵，则对每一 $\Bbb R^n$ 中的 $\mathbf b$，方程 $Ax = \mathbf b$ 有惟一解 $x = A^{(-1)}\mathbf b$

若 $A、B、 \cdots、 N$ 是 $n \times n$ 可逆矩阵，$AB \cdots N$ 也可逆。

\[(AB \cdots N)^{(-1)} = N^{(-1)} \cdots B^{(-1)} A^{(-1)}\]

若 $A$ 可逆，则 $A^T$ 也可逆

\[(A^T)^{(-1)} = (A^{(-1)})^T\]

2.3 可逆矩阵的特征

定理 8 $\quad$ (可逆矩阵定理)

设 $A$ 为 $n \times n$ 矩阵，下列命题等价，即它们同时为真或同时为假

1. $A$ 是可逆矩阵
2. $A$ 等价于 $n \times n$ 单位矩阵
3. $A$ 有 $n$ 个主元位置
4. 方程 $Ax=0$ 仅有平凡解
5. $A$ 的各列线性无关
6. 线性变换 $x \mapsto Ax$ 是一对一的
7. 对 $\Bbb R^n$ 中任意 $b$, 方程 $Ax=b$ 至少有一个解
8. $A$ 的各列生成 $\Bbb R^n$
9. 线性变换 $x \mapsto Ax$ 把 $\Bbb R^n$ 映射到 $\Bbb R^n$ 上
10. 存在 $n \times n$ 矩阵 $C$ 使 $CA=I$
11. 存在 $n \times n$ 矩阵 $D$ 使 $AD=I$
12. $A^T$ 是可逆矩阵

内积和外积

将 $\Bbb R^n$ 中向量看作 $n \times 1$ 矩阵，对 $\Bbb R^n$ 中的 $\mathbf{u, v}$，

• 矩阵乘积 $\mathbf u^T \mathbf v$ 是 $1 \times 1$ 矩阵，称为 $\mathbf u$ 和 $\mathbf v$ 的 内积或数量积;

• 矩阵乘积 $\mathbf{uv}^T$ 是 $n \times n$ 矩阵，称为 $\mathbf u$ 和 $\mathbf v$ 的 外积或向量积。

  \[\begin{aligned} \mathbf{uv}^T &= \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} [v_1 \quad v_2 \quad v_3] \\ &= \begin{bmatrix} \color{red}{u_1} & u_1 & u_1 \\ \color{red}{u_2} & u_2 & u_2 \\ \color{red}{u_3} & u_3 & u_3 \end{bmatrix} \odot \begin{bmatrix} \color{green}{v_1} & \color{green}{v_2} & \color{green}{v_3} \\ v_1 & v_2 & v_3 \\ v_1 & v_2 & v_3 \end{bmatrix} \\ &= \begin{bmatrix} \color{red}{u_1}\color{green}{v_1} & u_1\color{green}{v_2} & u_1\color{green}{v_3} \\ \color{red}{u_2}v_1 & u_2v_2 & u_2v_3 \\ \color{red}{u_3}v_1 & u_3v_2 & u_3v_3 \end{bmatrix} \end{aligned}\]

  octave 中可以用 meshgrid 函数得到 $\mathbf{u ,v}$ 的外积

2.4 分块矩阵

\[AB = A[\mathbf{b_1 \; b_2 \; \cdots b_n}] = [A\mathbf b_1 \; A\mathbf b_2 \; \cdots A\mathbf b_n]\]

计算 $AB$ 的行列法则

\[(AB)_{ij} = \sum_{r=1}^k a_{ir}b_{rj} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{ik}b_{kj}\]

定理 10 $\quad$ ($AB$ 的列行展开)

若 $A$ 是 $m \times n$ 矩阵，$B$ 是 $n \times p$ 矩阵，则

\[\begin{aligned} AB &= [\mathrm{col_1}(A) \quad \mathrm{col_2}(A) \quad \cdots \quad \mathrm{col_n}(A)] \begin{bmatrix} \mathrm{row_1}(B) \\ \mathrm{row_2}(B) \\ \vdots \\ \mathrm{row_n}(B) \\ \end{bmatrix} \\ &= \mathrm{col_1}(A)\mathrm{row_1}(B) + \mathrm{col_2}(A)\mathrm{row_2}(B) + \cdots + \mathrm{col_n}(A)\mathrm{row_n}(B) \end{aligned}\]

上面每一项的乘积 $\mathrm{col_k}(A)\mathrm{row_k}(B)$ 都是外积。

2.8 $\Bbb R^n$ 的子空间

定义 $\quad$ $\Bbb R^n$ 中的一个子空间是 $\Bbb R^n$ 中的集合 $H$，具有以下三个性质，

1. 零向量属于 $H$
2. 对 $H$ 中的任意向量 $\mathbf{u}$ 和 $\mathbf{v}$，$\mathbf{u+v}$ 属于 $H$
3. 对 $H$ 中的任意向量 $\mathbf{u}$ 和数 $c$，$c\mathbf{u}$ 属于 $H$

换句话说，子空间对加法和标量乘法是封闭的。注意 $\Bbb R^n$ 是它本身的子空间。

设 $\mathbf{v_1,\cdots,v_p}$ 属于 $\Bbb R^n$，$\mathbf{v_1,\cdots,v_p}$ 的所有线性组合是 $\Bbb R^n$ 的子空间，也就是说，$H = \mathbf{Span}\{\mathbf{v_1,\cdots,v_p}\}$，则 $H$ 是 $\Bbb R^n$ 的子空间。我们称 $\mathbf{Span}\{\mathbf{v_1,\cdots,v_p}\}$ 为由 $\mathbf{v_1,\cdots,v_p}$ 生成(或张成)的子空间。

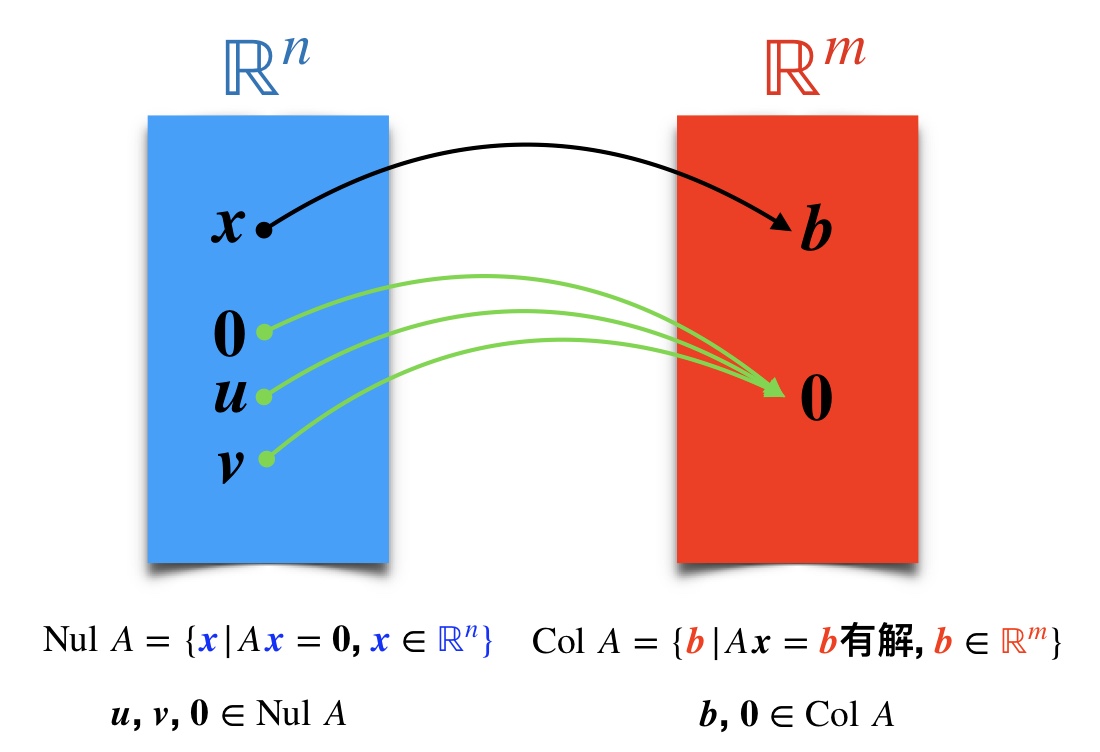
矩阵的列空间与零空间

列空间定义 $\quad$ 矩阵 $A$ 的列空间是 $A$ 的各列的线性组合的集合，记作 $\mathrm{Col}\;A$

$m \times n$ 矩阵 $A=[\mathbf{a}_1,\cdots,\mathbf{a}_n]$，它的各列属于 $\Bbb R^m$，列空间是 $\Bbb R^m$ 的子空间。

零空间定义 $\quad$ 矩阵 $A$ 的零空间是齐次方程 $A\mathbf{x}=0$ 所有解的集合，记为 $\mathrm{Nul}\;A$

当 $A$ 有 $n$ 列时，$Ax=0$ 的解属于 $\Bbb R^n$，$A$ 的零空间是 $\Bbb R^n$ 上的子集。

定理 12 $\quad$ $m \times n$ 矩阵 $A$ 的零空间是 $\Bbb R^n$ 的子空间。等价的，$n$ 个未知数的 $m$ 个齐次线性方程的解的全体是 $\Bbb R^n$ 的子空间。

这里要注意，$m \times n$ 矩阵 $A$ 的列空间是所有使方程 $Ax=b$ 有解的向量 $\mathbf{b}$ 的集合，属于 $\Bbb R^m$。零空间是齐次方程 $A\mathbf{x}=0$ 所有的解向量 $\mathbf{x}$ 的集合，属于 $\Bbb R^n$。

从映射的角度看 $T: \Bbb R^n \to \Bbb R^m$，列空间属于值域(值域是余定义域 $\Bbb R^m$ 上的子集)，零空间属于定义域 $\Bbb R^n$ 上的子集。

子空间的基

定义 $\quad$ $\Bbb R^n$ 中子空间 $H$ 的一组基是 $H$ 中的一个线性无关集，它生成 $H$

矩阵 $A$ 的主元列构成列空间的基。

2.9 维数与秩

坐标系

定义 $\quad$ 假设 $\mathcal{B} = [\mathbf{b_1,\cdots,b_p}]$ 是子空间 $H$ 的一组基，对 $H$ 中的每一个向量 $\mathbf x$，相对于基 $\mathcal{B}$ 的坐标是使 $\mathbf{x} = c_1\mathbf{b}_1 + \cdots + c_p\mathbf{b}_p$ 成立的权值 $c_1,\cdots,c_p$，且是 $\Bbb R^p$ 中的向量

\[[\mathbf{x}]_{\mathcal{B}} = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_p \end{bmatrix}\]

称为 $\mathbf{x}$ (相对于 $\mathcal{B}$) 的坐标向量，或 $\mathbf{x}$ 的 $\mathcal{B}$-坐标向量。

注意，$H$ 的一组基 $\mathcal{B}$ 确定 $H$ 上的一个“坐标系”，不同的基表示 $H$ 的不同坐标系。因此 $H$ 中的一个向量 $\mathbf{x}$ 在不同的基上对应不同的坐标向量。

一般的，如果 $\mathcal{B} = \{\mathbf b_1,\cdots,\mathbf b_p\}$ 是 $H$ 的基，则映射 $x \mapsto [x]_{\mathcal{B}}$ 是使 $H$ 和 $\Bbb R^p$ 形态一样的一一映射($H$ 中向量的元素个数有可能多于 $p$ 个)，且 $H$ 与 $\Bbb R^p$ 同构。

子空间的维数

维数定义 $\quad$ 非零子空间 $H$ 的维数，用 $\dim H$ 表示，是 $H$ 的任意一个基的向量个数，零子空间 $\{\mathbf 0\}$ 的维数定义为零。

• $\Bbb R^n$ 空间维数为 $n$，$\Bbb R^n$ 的每个基由 $n$ 个向量组成。
• 矩阵 $A$ 的零空间 $\mathrm{Nul}A$ 的维数，等于 $A\mathbf x = \mathbf 0$ 中自由变量的个数。

秩的定义 $\quad$ 矩阵 $A$ 的秩(记为 rank $A$)是 $A$ 的列空间的维数。

\[\mathrm{rank}A = \dim \mathrm{Col}A\]

• $A$ 的主元列形成 $\mathrm{Col}A$ 的一个基，$A$ 的秩正好是 $A$ 的主元列个数。
• 非主元列对应于 $Ax=0$ 中自由变量的个数，$\mathrm{Nul}A$ 的维数正好是非主元列的个数。

定理 14 $\quad$ (秩定理)

如果矩阵 $A$ 有 $n$ 列，则 $\mathrm{rank}A + \dim\mathrm{Nul}A = n$.

定理 15 $\quad$ (基定理)

设 $H$ 是 $\Bbb R^n$ 的 $p$ 维子空间，$H$ 中的任何恰好由 $p$ 个成员组成的线性无关集构成 $H$ 的一个基. 并且，$H$ 中任何生成 $H$ 的 $p$ 个向量集也构成 $H$ 的一个基。

秩与可逆矩阵定理

定理 $\quad$ (可逆矩阵定理 (续))

设 $A$ 是一 $n \times n$ 矩阵，则下面每个命题与 $A$ 是可逆矩阵的命题等价:

13. $A$ 的列向量构成 $\Bbb R^n$ 的一个基
14. $\mathrm{Col}A = \Bbb R^n$
15. $\dim\mathrm{Col}A = n$
16. $\mathrm{rank}A = n$
17. $\mathrm{Nul}A = {0}$
18. $\dim\mathrm{Nul}A = 0$

三、行列式

3.1 行列式介绍

对于 $1 \times 1$ 矩阵，设 $A=[a]$，定义 $\det A = a$.

对于 $2 \times 2$ 矩阵，设 $A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}$，定义 $\det A = ad-bc$

当 $n \ge 2$，$n \times n$ 矩阵 $A=[a_{ij}]$ 的行列式的定义如下:

\[\begin{aligned} \det A &= a_{11}\cdot\det A_{11} - a_{12}\cdot\det A_{12} + \cdots + (-1)^{1+n}a_{1n}\cdot\det A_{1n} \\ &= \sum_{j=1}^n(-1)^{1+j}a_{1j}\det A_{1j} \end{aligned}\]

这里元素 $a_{11}, a_{12}, \cdots, a_{1n}$ 来自 $A$ 的第一行，$A_{11}, A_{12}, \cdots, A_{1n}$ 由 $A$ 中划去第一行和对应列得到，对任意方阵 $A$，令 $A_{ij}$ 表示通过划掉 $A$ 中第 $i$ 行和第 $j$ 列而得到的子矩阵。这给出了行列式的一个递归定义，当 $n=3$ 时，$\det A$ 由 $2 \times 2$ 子矩阵 $A_{1j}$ 的行列式来定义。

对于 $A=[a_{ij}]$，$A$ 的 $(i,j)$ 余因子 $C_{ij}$ 由下式给出

\[\color{red}{C_{ij} = (-1)^{i+j}\det A_{ij}}\]

则前面 $\det A$ 的定义可以改写为

\[\det A = a_{11} \cdot C_{11} + a_{12} \cdot C_{12} + \cdots + a_{1n} \cdot C_{1n}\]

这个公式称为按 $A$ 的第一行的余因子展开式。

定理 1 $\quad n \times n$ 矩阵 $A$ 的行列式可按任意行或列的余因子展开式来计算。

• 按第 $i$ 行展开

  \[\det A = a_{i1} \cdot C_{i1} + a_{i2} \cdot C_{i2} + \cdots + a_{in} \cdot C_{in}\]

• 按第 $j$ 列展开

  \[\det A = a_{1j} \cdot C_{1j} + a_{2j} \cdot C_{2j} + \cdots + a_{nj} \cdot C_{nj}\]

定理 2 $\quad$ 若 $A$ 为三角阵，则 $\det A$ 等于 $A$ 主对角线上元素的乘积。

3.2 行列式的性质

定理 3 $\quad$ (行变换)

令 $A$ 是一个方阵

$\quad$ a. $A$ 倍加变换后得矩阵 $B$，则 $\det B = \det A$

$\quad$ b. $A$ 对换变换后得矩阵 $B$，则 $\det B = -\det A$

$\quad$ c. $A$ 倍乘变换(k倍)后得矩阵 $B$，则 $\det B = k\cdot\det A$

若一个方阵 $A$ 被行倍加和行交换化简为阶梯形 $U$，且此过程经过了 $r$ 次行交换，则定理 3表明

\[\det A = (-1)^r \det U\]

由于 $U$ 是阶梯形，它是三角阵，因此 $\det U$ 是主对角线上元素 $u_{11},\cdots,u_{nn}$ 的乘积. 若 $A$ 可逆，则元素 $u_{ii}$ 都是主元. 否则，至少有 $u_{nn}$ 等于零，使得乘积 $u_{11} \cdots u_{nn}$ 为零。从而有以下公式

\[\det A = \begin{cases} (-1)^r \cdot u_{11} \cdot u_{22} \cdots u_{nn} & 当A可逆 \\ 0 & 当A不可逆 \end{cases}\]

定理 4 $\quad$ 方阵 $A$ 是可逆的当且仅当 $\det A \ne 0$

如果 $A$ 的列线性相关，则 $\det A = 0$

列变换

定理 5 $\quad$ 若 $A$ 为一个 $n \times n$ 矩阵，则 $\det A^T = \det A$

行列式与矩阵乘积

定理 6 $\quad$ (乘法的性质)

若 $A$ 和 $B$ 均为 $n \times n$ 矩阵，则 $\det AB = (\det A)(\det B)$

3.3 克拉默法则、体积和线性变换

定理 7 $\quad$ (克拉默法则)

设 $A$ 是一个 $n \times n$ 可逆矩阵，对 $\Bbb R^n$ 中任意向量 $b$，方程 $Ax=b$ 的惟一解可由下式给出

\[x_i = \dfrac{\det A_i(\mathbf b)}{\det A}, i=1,2,\cdots n\]

其中 $A_i(\mathbf b)$ 表示 $A$ 中第 $i$ 列由向量 $\mathbf b$ 替换得到的矩阵 $A_i(\mathbf b) = [a_1 \; \cdots \; \mathbf b \; \cdots \; a_n]$

一个求 $A^{-1} 的公式$

\[A^{-1} = \dfrac{1}{\det A} \begin{bmatrix} C_{11} & C_{21} & \cdots & C_{n1} \\ C_{12} & C_{22} & \cdots & C_{n2} \\ \vdots & \vdots & \cdots & \vdots \\ C_{1n} & C_{2n} & \cdots & C_{nn} \end{bmatrix}\]

上式右边余因子的矩阵称为 $A$ 的伴随矩阵，记为 $\mathrm{adj}A$

定理 8 $\quad$ (逆矩阵公式)

设 $A$ 是一个可逆 $n \times n$ 矩阵，则 $A^{-1}=\dfrac{1}{\det A}\mathrm{adj}A$.

用行列式表示面积或体积

定理 9 $\quad$ 若 $A$ 是一个 $2 \times 2$ 矩阵，则由 $A$ 的列确定的平行四边形的面积为 $|\det A|$，若 $A$ 是一个 $3 \times 3$ 矩阵，则由 $A$ 的列确定的平行六面体的体积为 $|\det A|$。

例如 $A$ 为 $2 \times 2$ 对角矩阵，则

\[\left|\det\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}\right| = |ad| = 矩阵的面积\]

若 $A$ 不为对角矩阵，通过倍加和对换变换，总可以使 $A$ 变换成对角矩阵。

线性变换

定理 10 $\quad$ 设 $T: \Bbb R^2 \to \Bbb R^2$ 是一个由 $2 \times 2$ 矩阵 $A$ 确定的线性变换，若 $S$ 是 $\Bbb R^2$ 中的一个平行四边形，则

\[\{T(S)的面积\} = |\det A| \cdot \{S的面积\}\]

对于 $\Bbb R^3$，则

\[\{T(S)的体积\} = |\det A| \cdot \{S的体积\}\]

定理 10 的结论对 $\Bbb R^2$ 中任意有限面积的区域或 $\Bbb R^3$ 中任意有限体积的区域均成立。

四、向量空间

4.1 向量空间与子空间

定义 $\quad$ 一个向量空间是由一些被称为向量的对象构成的非空集合 $V$，在这个集合上定义两个运算，称为加法和标量乘法(标量取实数)，服从以下公理(或法则)，这些公理必须对 $V$ 中所有向量 $\mathbf{u,v,w}$及所有标量 $c$ 和 $d$ 均成立。

1. $\mathbf{u,v}$ 之和表示为 $\mathbf{u+v}$，仍在 $V$ 中
2. $\mathbf{u+v = v+u}$ (加法交换律, commutativity)
3. $\mathbf{(u+v)+w = u+(v+w)}$ (加法结合律, associativity)
4. $V$ 中存在一个零向量 $\mathbf{0}$，使得 $\mathbf{u+0=u}$
5. 对 $V$ 中每个向量 $\mathbf{u}$，存在 $V$ 中向量 $-\mathbf{u}$，使得 $\mathbf{u+(-u)=0}$ (加法逆元, additive inverse)
6. $\mathbf{u}$ 与标量 $c$ 的标量乘法记为 $c\mathbf{u}$，仍在 $V$ 中
7. $c\mathbf{(u+v)}=c\mathbf{u}+c\mathbf{v}$ (分配性质, distributive property)
8. $(c+d)\mathbf{u}=c\mathbf{u}+d\mathbf{u}$ (分配性质, distributive property)
9. $c(d\mathbf{u})=(cd)\mathbf{u}$ (乘法结合律, associativity)
10. $1\mathbf{u}=\mathbf{u}$ (单位元, identities)

子空间

定义 $\quad$ 向量空间 $V$ 中的一个子空间是 $V$ 的一个满足以下三个性质的子集 $H$:

1. $V$ 中的零向量在 $H$ 中
2. $H$ 对向量加法封闭，即对 $H$ 中任意向量 $\mathbf{u,v}$，和$\mathbf{u+v}$ 仍在 $H$ 中
3. $H$ 对标量乘法封闭，即对 $H$ 中任意向量 $\mathbf{u}$ 和任意标量 $\mathbf{c}$，向量$c\mathbf{u}$ 仍在 $H$ 中

向量空间 $V$ 中仅由零向量组成的集合是 $V$ 的一个子空间，称为零子空间，写成 {$\mathbf{0}$}。

向量空间 $\Bbb R^2$ 不是 $\Bbb R^3$ 的子空间，因为 $\Bbb R^2$ 甚至不是 $\Bbb R^3$ 的子集( $\Bbb R^3$ 中的向量有3个分量，而 $\Bbb R^2$ 中的向量仅有两个分量)，集合

\[H = \left\{ \begin{bmatrix} s \\ t \\ 0 \end{bmatrix} : s,t是实数 \right\}\]

是 $\Bbb R^3$ 的一个子集。

定理 1 $\quad$ 若 $\mathbf{v_1,\cdots,v_p}$ 是在向量空间 $V$ 中，则 $\mathbf{Span}\{v_1,\cdots,v_p\}$ 是 $V$ 的一个子空间。

4.2 零空间、列空间和线性变换

矩阵的零空间

定义 $\quad m \times n$ 矩阵 $A$ 的零空间写成 $\mathrm{Nul}A$，是齐次方程 $A\mathbf{x}=\mathbf{0}$ 的全体解的集合，用集合符号表示，即 \(\mathrm{Nul}A = \{\mathbf{x}:\mathbf{x} \in \Bbb R^n,A\mathbf{x}=\mathbf{0}\}\)

定理 2 $\quad$ $m \times n$ 矩阵 $V$ 的零空间是 $\Bbb R^n$ 的一个子空间。

矩阵的列空间

定义 $\quad m \times n$ 矩阵的列空间写成 $\mathrm{Col}A$ 是由 $A$ 的列的所有线性组合组成的集合，若 $A = [\mathbf{a_1,\cdots,a_n}]$，则 $\mathrm{Col}A=\mathbf{Span}\{\mathbf{a_1,\cdots,a_n}\}$

定理 3 $\quad m \times n$ 矩阵 $A$ 列空间是 $\Bbb R^m$ 的一个子空间。

\[\mathrm{Col}A = \{\mathbf{b}:\mathbf{b}=A\mathbf{x},\mathbf{x} \in \Bbb R^n\}\]

对 $m \times n$ 矩阵 $A$，$\mathrm{Nul}A$ 与 $\mathrm{Col}A$ 的对比

$\mathrm{Nul}A$	$\mathrm{Col}A$
1. $\mathrm{Nul}A$ 是 $\Bbb R^n$ 的一个子空间	1. $\mathrm{Col}A$ 是 $\Bbb R^m$ 的一个子空间
2. $\mathrm{Nul}A$ 是隐式定义的，即只给出了一个 $\mathrm{Nul}A$ 中向量必须满足的条件( $A\mathbf{x}=\mathbf{0}$ )	2. $\mathrm{Col}A$ 是显示定义，即明确指出如何建立 $\mathrm{Col}A$ 中的向量
3. 求 $\mathrm{Nul}A$ 中的向量需要时间，需要对 $[A \mathbf{0}]$ 做行变换	3. 容易求出 $\mathrm{Col}A$ 中的向量，$A$ 中的列就是 $\mathrm{Col}A$ 中的向量，其余的可由 $A$ 的列表示出来
4. $\mathrm{Nul}A$ 与 $A$ 的数值之间没有明显关系	4. $\mathrm{Col}A$ 与 $A$ 的数值之间有明显的关系，因为 $A$ 的列就在 $\mathrm{Col}A$ 中
5. $\mathrm{Nul}A$ 中的一个典型向量 $v$ 具有 $A\mathbf{v}=\mathbf{0}$ 的性质	5. $\mathrm{Col}A$ 中的一个典型向量 $v$ 具有方程 $A\mathbf{x}=\mathbf{v}$ 是相容的性质
6. 给一个特定的向量 $\mathbf{v}$，容易判断 $\mathbf{v}$ 是否在 $\mathrm{Nul}A$ 中，只需要计算 $A\mathbf{v}$	6. 给定一个特定的向量 $\mathbf{v}$，弄清 $\mathbf{v}$ 是否在 $\mathrm{Col}A$ 中需要时间，需要对 $[A\;\mathbf{v}]$ 作行变换
7. $\mathrm{Nul}A = \{\mathbf{0}\}$ 当且仅当方程 $A\mathbf{x}=\mathbf{0}$ 仅有平凡解	7. $\mathrm{Col}A = \Bbb R^m$ 当且仅当方程 $A\mathbf{x}=\mathbf{b}$ 对每个 $\mathbf{b} \in \Bbb R^m$ 有一个解
8. $\mathrm{Nul}A=\{0\}$ 当且仅当线性变换 $\mathbf{x} \to A\mathbf{x}$ 是一对一的	8. $\mathrm{Col}A = \Bbb R^m$ 当且仅当线性变换 $\mathbf{x} \to A\mathbf{x}$ 将 $\Bbb R^n$ 映射到 $\Bbb R^m$ 上

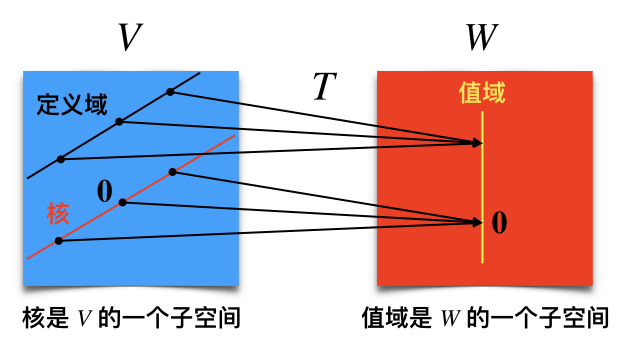
线性变换的核与值域

定义 $\quad$ 由向量空间 $V$ 映射到向量空间 $W$ 内的线性变换 $T$ 是一个规则，它将 $V$ 中每个向量 $\mathbf{x}$ 映射成 $W$ 中惟一向量 $T(\mathbf{x})$，且满足:

1. $T(\mathbf{u+v})=T(\mathbf{u})+T(\mathbf{v})$，对 $V$ 中所有 $\mathbf{u,v}$ 均成立.
2. $T(c\mathbf{u})=cT(\mathbf{u)}$，对 $V$ 中所有 $\mathbf{u}$ 及所有数 $c$ 均成立.

线性变换 $T$ 的核 (或零空间) 是 $V$ 中所有满足 $T(\mathbf{u})=\mathbf{0}$ 的向量 $\mathbf{u}$ 的集合 ($\mathbf{0}$ 为 $W$ 中的零向量). $T$ 的值域是 $W$ 中所有具有形式 $T(\mathbf{x})$ (任意 $\mathbf{x} \in V$) 的向量的集合. 如果 $T$ 是由一个矩阵变换得到的，比如对某矩阵 $A$，$T(\mathbf{x}=A\mathbf{x})$，则 $T$ 的核与值域恰好是 $A$ 的零空间和列空间。

4.3 线性无关集和基

定理 4 $\quad$ 不少于两个有编号的向量的集合 $\{\mathbf{v_1,\cdots,v_p}\}$，如果有 $\mathbf{v_1 \ne 0}$，则 $\{\mathbf{v_1,\cdots,v_p}\}$ 是线性相关的，当且仅当某 $\mathbf{v}_j(j\gt1)$ 是其前面向量 $\mathbf{v_1,\cdots,v_{j-1}}$ 的线性组合。

定义 $\quad$ 令 $H$ 是向量空间 $V$ 的一个子空间，$V$ 中向量的指标集 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_p}\}$ 称为 $H$ 的一个基，如果

1. $\mathcal{B}$ 是线性无关集
2. 由 $\mathcal{B}$ 生成的子空间与 $H$ 相同，即 $H = \mathbf{Span}\{\mathbf{b_1,\cdots,b_p}\}$

令 $\mathbf{e_1,\cdots,e_n}$ 是 $n \times n$ 单位矩阵 $I_n$ 的列，集合 $\{\mathbf{e_1,\cdots,e_n}\}$ 称为 $\Bbb R^n$ 的标准基。

一个基是一个不包含不必要的向量的“高效率”的生成集(Spanning Set)。

定理 5 $\quad$ (生成集定理 Spanning Set Theorem)

若 $S=\{\mathbf{v_1,\cdots,v_p}\}$ 是 $V$ 中的向量集，$H=\mathbf{Span}\{\mathbf{v_1,\cdots,v_p}\}$

a. 若 $S$ 中某一向量，比如说 $\mathbf{v}_k$，是 $S$ 中其余向量的线性组合，则 $S$ 中去掉 $\mathbf{v}_k$ 后形成的集合仍然可以生成 $H$

b. 若 $H\ne\{\mathbf{0}\}$，则 $S$ 的某一子集是 $H$ 的一个基

$\mathrm{Nul}A$ 和 $\mathrm{Col}A$ 的基

矩阵的行初等变换不影响矩阵的列的线性相关关系

定理 6 $\quad$ 矩阵 $A$ 的主元列构成 $\mathrm{Col}A$ 的一个基

4.4 坐标系

对一个向量空间 $V$，明确指定一个基 $\mathcal{B}$ 的重要原因是在 $V$ 上强加一个“坐标系”，如果 $\mathcal{B}$ 包含 $n$ 个向量，则坐标系将使 $V$ 像 $\Bbb R^n$ 一样便于操作。

定理 7 $\quad$ (惟一表示定理)

令 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$ 是向量空间 $V$ 的一个基，则对 $V$ 中每个向量 $\mathbf{x}$，存在惟一的一组数 $c_1,\cdots,c_n$，使得

\[\mathbf{x} = \color{fuchsia}{c_1}\mathbf{b_1} + \cdots + \color{fuchsia}{c_n}\mathbf{b_n}\]

定义 $\quad$ 假设集合 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$ 是 $V$ 的一个基，$\mathbf{x}$ 在 $V$ 中，$\mathbf{x}$ 相对于基 $\mathcal{B}$ 的坐标(或 $\mathbf{x}$ 的 $\mathcal{B}$-坐标)是使得 $\mathbf{x} = c_1\mathbf{b_1} + \cdots + c_n\mathbf{b_n}$ 的权 $c_1,\cdots,c_n$

若 $c_1,\cdots,c_n$ 是 $\mathbf{x}$ 的 $\mathcal{B}$-坐标，则 $\Bbb R^n$ 中的向量

\[[\mathbf{x}]_{\mathcal{B}} = \begin{bmatrix} \color{fuchsia}{c_1} \\ \vdots \\ \color{fuchsia}{c_n} \end{bmatrix}\]

是 $\mathbf{x}$ (相对于 $\mathcal{B}$) 的坐标向量，或 $\mathbf{x}$ 的 $\mathcal{B}$-坐标向量，映射 $\mathbf{x} \mapsto [\mathbf{x}]_{\mathcal{B}}$ 称为 (由 $\mathcal{B}$ 确定的) 坐标映射。

$\Bbb R^n$ 中的坐标

令

\[P_{\mathcal{B}} = [\mathbf{b_1\;b_2\;\cdots\;b_n}]\]

则向量方程

\[\mathbf{x} = \color{fuchsia}{c_1}\mathbf{b_1} + \color{fuchsia}{c_2}\mathbf{b_2} + \cdots + \color{fuchsia}{c_n}\mathbf{b_n}\]

等价于

\[\mathbf{x} = P_{\mathcal{B}}\color{fuchsia}{[\mathbf{x}]_{\mathcal{B}}}\]

我们称 $P_{\mathcal{B}}$ 为从 $\mathcal{B}$ 到 $\Bbb R^n$ 中标准基的坐标变换矩阵。通过左乘 $P_{\mathcal{B}}$ 将坐标向量 $[\mathbf{x}]_{\mathcal{B}}$ 变换到 $\mathbf{x}$。由于 $P_{\mathcal{B}}$ 的列构成 $\Bbb R^n$ 的一个基，$P_{\mathcal{B}}$ 是可逆的. 通过左乘 $P^{-1}_{\mathcal{B}}$ 又将 $\mathbf{x}$ 变回 $\mathcal{B}$-坐标向量:

\[P^{-1}_{\mathcal{B}}\mathbf{x} = [\mathbf{x}]_{\mathcal{B}}\]

坐标映射 $\mathbf{x} \mapsto [\mathbf{x}]_{\mathcal{B}}$ 对应的矩阵即 $P^{-1}_{\mathcal{B}}$.

\[\require{AMScd} \begin{CD} \mathbf{x} @>{P^{-1}_{\mathcal{B}} (\mathcal{B}坐标向量})>> [\mathbf{x}]_{\mathcal{B}} \\ @VVV @VVV \\ 标准坐标向量 @<<{P_{\mathcal{B}} (标准坐标向量)}< \mathcal{B}坐标向量 \end{CD}\]

可以行化简增广矩阵 $[P_{\mathcal{B}} \quad \mathbf{x}]$ 来求解 $[\mathbf{x}]_{\mathcal{B}}$ 而不必计算 $P^{-1}_{\mathcal{B}}$.

坐标映射

定理 8 $\quad$ 令 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$ 是向量空间 $V$ 的一个基，则坐标映射 $\mathbf{x} \mapsto [\mathbf{x}]_{\mathcal{B}}$ 是一个由 $V$映上到 $\Bbb R^n$ 的一对一的线性变换。

一般而言，从一个向量空间 $V$ 映上到另一个向量空间 $W$ 的一对一线性变换称为从 $V$ 到 $W$ 上的一个 同构(isomorphism)，每一个在向量空间 $V$ 中的计算可以完全相同的出现在 $W$ 中，反之亦然。

例如，向量空间 $V$ 可以是:

• 多项式空间 $\Bbb P_3$ 到 $\Bbb R^4$ 上的同构
• $\Bbb R^3$ 中的一个2维平面到 $\Bbb R^2$ 上的同构
• $\Bbb R^n$ 到 $\Bbb R^n$ 上的同构 (不同的基)

4.5 向量空间的维数

定理 9 $\quad$ 若向量空间 $V$ 具有一组基 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$，则 $V$ 中任意包含多于 $n$ 个向量的集合一定线性相关.

定理 10 $\quad$ 若向量空间 $V$ 有一组基含有 $n$ 个向量，则 $V$ 的每一组基一定恰好含有 $n$ 个向量.

定义 $\quad$ 若 $V$ 由一个有限集生成，则 $V$ 称为有限维的，$V$ 的维数写成 $\dim V$，是 $V$ 的基中含有的向量个数，零向量空间 $\{\mathbf{0}\}$ 的维数定义为零. 如果 $V$ 不是由一个有限集生成，则 $V$ 称为无穷维的.

$\Bbb R^n$ 的标准基含有 $n$ 个向量，所以 $\dim \Bbb R^n = n$，标准的多项式基 {$1,t,t^2$} 表明 $\dim \Bbb P^2 = 3$，一般而言，$\dim \Bbb P^n = n+1$，所有多项式的空间 $\Bbb P$ 是无穷维的。

有限维空间的子空间

定理 11 $\quad$ 令 $H$ 是有限维向量空间 $V$ 的子空间，若有需要的话，$H$ 中任一个线性无关集均可以扩充为 $H$ 的一个基，$H$ 也是有限维的并且

\[\dim H \le \dim V\]

定理 12 $\quad$ (基定理)

令 $V$ 是一个 $p$ 维向量空间，$p \ge 1$，$V$ 中任意含有 $p$ 个元素的线性无关集必须是 $V$ 的一个基. 任意含有 $p$ 个元素且生成 $V$ 的集合必须是 $V$ 的一个基.

$\mathrm{Nul}A$ 和 $\mathrm{Col}A$ 的维数

$\mathrm{Nul}A$ 的维数是方程 $A\mathbf{x}=\mathbf{0}$ 中自由变量的个数，$\mathrm{Col}A$ 的维数是 $A$ 中主元列的个数.

4.6 秩

行空间

若 $A$ 是一个 $m \times n$ 矩阵，$A$ 的每一行具有 $n$ 个数字，即可以视为 $\Bbb R^n$ 中的向量. 其行向量的所有线性组合的集合称为 $A$ 的 行空间，记为 $\mathrm{Row}A$.

定理 13 $\quad$ 若两个矩阵 $A$ 和 $B$ 行等价，则它们的行空间相同. 若 $B$ 是阶梯形矩阵，则 $B$ 的非零行构成 $A$ 的行空间的一个基同时也是 $B$ 的行空间的一个基.

警告 $\quad$ 行变换对矩阵的行不保持线性相关关系，若矩阵 $A$ 和 $B$ 行等价，$B$ 的行线性无关不能保证 $A$ 的行线性无关.

秩定理

定义 $\quad$ $A$ 的秩即 $A$ 的列空间的维数.

由于 $\mathrm{Row}A$ 与 $\mathrm{Col}A^T$ 相同，则 $A$ 的行空间的维数等于 $A^T$ 的秩.

定理 14 $\quad$ (秩定理)

$m \times n$ 矩阵 $A$ 的列空间和行空间的维数相等，这个公共的维数(即 $A$ 的秩)还等于 $A$ 的主元位置的个数且满足方程

\[\mathrm{rank}A + \dim \mathrm{Nul}A = n\]

$\mathrm{rank}A$ 是 $A$ 中主元列的个数，$\mathrm{Nul}A$ 的维数是 $A$ 中非主元列的个数，显然有

\[主元列个数 + 非主元列个数 = 列的个数\]

定理 $\quad$ (可逆矩阵定理 (续))

设 $A$ 是一 $n \times n$ 矩阵，则下面每个命题与 $A$ 是可逆矩阵的命题等价:

13. $A$ 的列向量构成 $\Bbb R^n$ 的一个基
14. $\mathrm{Col}A = \Bbb R^n$
15. $\dim\mathrm{Col}A = n$
16. $\mathrm{rank}A = n$
17. $\mathrm{Nul}A = {0}$
18. $\dim\mathrm{Nul}A = 0$

4.7 基的变换

定理 15 $\quad$ 设 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$ 和 $\mathcal{C}=\{\mathbf{c_1,\cdots,c_n}\}$ 是向量空间 $V$ 的基，则存在一个 $n \times n$ 矩阵 $\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}$ 使得

\[\begin{aligned} [\mathbf{x}]_{\mathcal{C}} &= \mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}} [\mathbf{x}]_{\mathcal{B}} \\[2ex] r_1\mathbf{c_1} + \cdots + r_n\mathbf{c_n} &= s_1[\mathbf{b_1}]_{\mathcal{C}} + \cdots + s_n[\mathbf{b_n}]_{\mathcal{C}} \\[2ex] r_1\mathbf{c_1} + \cdots + r_n\mathbf{c_n} &= s_1(t_{11}\mathbf{c_1} + \cdots + t_{1n}\mathbf{c_n}) + \cdots + s_n(t_{n1}\mathbf{c_1} + \cdots + t_{nn}\mathbf{c_n}) \end{aligned}\]

其中

\[[\mathbf{x}]_{\mathcal{C}} = \begin{bmatrix} r_1 \\ \vdots \\ r_n \end{bmatrix} \qquad [\mathbf{x}]_{\mathcal{B}} = \begin{bmatrix} s_1 \\ \vdots \\ s_n \end{bmatrix} \qquad [\mathbf{b_1}]_{\mathcal{C}} = \begin{bmatrix} t_{11} \\ \vdots \\ t_{1n} \end{bmatrix} \qquad \cdots \qquad [\mathbf{b_n}]_{\mathcal{C}} = \begin{bmatrix} t_{n1} \\ \vdots \\ t_{nn} \end{bmatrix}\]

$\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}$ 的列是基 $\mathcal{B}$ 中向量的 $\mathcal{C}$-坐标向量，即

\[\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}} = [[\mathbf{b_1}]_{\mathcal{C}} \; [\mathbf{b_2}]_{\mathcal{C}} \; \cdots \; [\mathbf{b_n}]_{\mathcal{C}}]\]

矩阵 $\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}$ 称为由 $\mathcal{B}$ 到 $\mathcal{C}$ 的坐标变换矩阵。

上式中矩阵 $\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}$ 的列是线性无关的，因为它们是线性无关集 $\mathcal{B}$ 的坐标向量，于是得到 $\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}$ 是可逆的.

\[\left(\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}\right)^{-1}[\mathbf{x}]_{\mathcal{C}} = [\mathbf{x}]_{\mathcal{B}}\]

于是 $\left(\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}\right)^{-1}$ 是将 $\mathcal{C}$-坐标变换 $\mathcal{B}$-坐标的矩阵，即

\[\left(\mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}\right)^{-1} = \mathop{P}\limits_{\mathcal{C} \gets \mathcal{B}}\]

$\Bbb R^n$ 中基的变换

若 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\}$，$\mathcal{E}$ 是 $\Bbb R^n$ 中的标准基 $\{\mathbf{e_1,\cdots,e_n}\}$，则 $[\mathbf{b_1}]_{\mathcal{E}}=\mathbf{b_1}$，因此，$\mathop{P}\limits_{\mathcal{E} \gets \mathcal{B}}$ 与坐标变换矩阵 $P_{\mathcal{B}}$ 相同，即

\[\mathop{P}\limits_{\mathcal{E} \gets \mathcal{B}} = [[\mathbf{b_1}]_{\mathcal{E}} \; [\mathbf{b_2}]_{\mathcal{E}} \; \cdots \; [\mathbf{b_n}]_{\mathcal{E}}] = [\mathbf{b_1} \; \mathbf{b_2} \; \cdots \; \mathbf{b_n}] = P_{\mathcal{B}}\]

五、特征值与特征向量

5.1 特征向量与特征值

定义 $\quad$ $A$ 为 $n \times n$ 矩阵，$\mathbf{x}$ 为非零向量，若存在数 $\lambda$ 使 $A\color{#08f}{\mathbf{x}} = \color{#f0f}{\lambda}\color{#08f}{\mathbf{x}}$ 成立，则称 $\color{#f0f}{\lambda}$ 为 $A$ 的特征值，$\color{#08f}{\mathbf{x}}$ 称为对应于 $\color{#f0f}{\lambda}$ 的特征向量.

数 $\lambda$ 是 $A$ 的特征值当且仅当方程

\[(A - \color{#f0f}{\lambda}I)\color{#08f}{\mathbf{x}} = \mathbf{0}\]

有非平凡解. 这个问题等价于要求出所有的 $\lambda$，使得矩阵 $A-\lambda I$ 为不可逆矩阵，由2.4节定理4，该矩阵当它的行列式的值为零时是不可逆的，即 $\det(A-\lambda I)=0$. 该方程所有解的集合就是矩阵 $A - \lambda I$ 的零空间，称为 $A$ 的对应于 $\lambda$ 的特征空间. 特征空间由零向量和所有对应于 $\lambda$ 的特征向量组成.

定理 1 $\quad$ 三角矩阵的主对角线的元素是其特征值.

$0$ 是 $A$ 的特征值当且仅当 $A$ 为不可逆.

定理 2 $\quad$ $\lambda_1,\cdots,\lambda_r$ 是 $n \times n$ 矩阵 $A$ 相异的特征值, $\mathbf{v_1,\cdots,v_r}$ 是与 $\lambda_1,\cdots,\lambda_r$ 对应的特征向量，那么向量集合 $\{\mathbf{v_1,\cdots,v_r}\}$ 线性无关.

5.2 特征方程

定理 $\quad$ (可逆矩阵定理 (续))

设 $A$ 是 $n \times n$ 矩阵，则 $A$ 是可逆的当且仅当

19. $0$ 不是 $A$ 的特征值.
20. $A$ 的行列式不等于零.

定理 3 $\quad$ (行列式的性质)

设 $A$ 和 $B$ 是 $n \times n$ 矩阵.

1. $A$ 可逆的充要条件是 $\det A \ne 0$.
2. $\det AB = (\det A)(\det B)$.
3. $\det A^T = \det A$.
4. 若 $A$ 是三角形矩阵，那么 $\det A$ 是 $A$ 主对角线元素的乘积.
5. 对 $A$ 作行替换不改变行列式的值. 作一次行交换使行列式值符号改变一次. 数乘一行后，行列式值等于用此数乘原来的行列式值.

特征方程

利用定理 3(1)，我们可以通过行列式来判断矩阵 $A - \lambda I$ 是否可逆. 数值方程 $\color{red}{\det (A-\lambda I) = 0}$ 称为 $A$ 的特征方程.

\[\boxed{数 \lambda 是 n \times n 矩阵 A 的特征值的充要条件是 \lambda 是特征方程 \det(A - \lambda I) = 0 的根.}\]

如果 $A$ 是 $n \times n$ 矩阵，那么 $\det(A-\lambda I)$ 是 $n$ 次多项式，称为 $A$ 的特征多项式.

一般的，$A$ 的特征方程的根 $r$ 的重数称为特征值 $r$ 的 (代数) 重数. 某 $6 \times 6$ 矩阵的特征多项式是 $\lambda^6-4\lambda^5-12\lambda^4$，因式分解后

\[\lambda^6-4\lambda^5-12\lambda^4 = \lambda^4(\lambda^2-4\lambda-12) = \lambda^4(\lambda-6)(\lambda+2)\]

该矩阵的特征值是 $0$ (重数为 $4$)，$6$ (重数为 $1$) 和 $-2$ (重数为 $1$).

因为 $n \times n$ 矩阵的特征方程包含有一个 $n$ 次多项式，如果算上重根，并允许有复根，则特征方程恰好有 $n$ 个根，复根称为复特征值.

相似性

假如 $A$ 和 $B$ 是 $n \times n$ 矩阵，如果存在可逆矩阵 $P$，使得 $P^{-1}AP = B$，或等价地 $A = PBP^{-1}$，则称 $A$ 相似于 $B$. 记 $Q = P^{-1}$，则有 $Q^{-1}BQ = A$，即 $B$ 也相似于 $A$，故我们简单的说 $A$ 和 $B$ 是相似的. 把 $A$ 变成 $P^{-1}AP$ 的变换称为相似变换.

定理 4 $\quad$ 若 $n \times n$ 矩阵 $A$ 和 $B$ 是相似的，那么他们有相同的特征多项式，从而有相同的特征值 (和相同的重数).

注意 $\quad$ 对矩阵作行变换通常会改变矩阵的特征值.

5.3 对角化

从分解式 $A = PDP^{-1}$，我们能够了解到有关矩阵 $A$ 的特征值和特征向量的信息. 分解式中的 $D$ 代表对角矩阵(Diagonal Matrix)，很容易计算出 $D$ 的幂.

\[\begin{array}{l} D = \begin{bmatrix} 5 & 0 \\ 0 & 3 \end{bmatrix} \\[2ex] D^2 = \begin{bmatrix} 5 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 5 & 0 \\ 0 & 3 \end{bmatrix} = \begin{bmatrix} 5^2 & 0 \\ 0 & 3^2 \end{bmatrix} \\[2ex] D^3 = DD^2 = \begin{bmatrix} 5 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 5^2 & 0 \\ 0 & 3^2 \end{bmatrix} \end{array}\]

一般地，有

\[对 k \ge 1, D^k = \begin{bmatrix} 5^k & 0 \\ 0 & 3^k \end{bmatrix}\]

若 $A=PDP^{-1}$，其中 $P$ 为可逆矩阵，$D$ 为对角矩阵，那么 $A^k$ 的计算会很简单.

\[\begin{array}{l} A = PDP^{-1} \\[2ex] A^2 = (PDP^{-1})(PDP^{-1}) = PD\underbrace{(P^{-1}P)}_{I}DP^{-1} = PDDP^{-1} = PD^2P^{-1} \\[2ex] A^3 = (PDP^{-1})A^2 = (PD\underbrace{P^{-1})P}_{I}D^2P^{-1} = PDD^2P^{-1} = PD^3P^{-1} \end{array}\]

一般地，有

\[A^k = PD^kP^{-1}\]

如果方阵 $A$ 相似于对角矩阵，即存在可逆矩阵 $P$ 和对角矩阵 $D$，有 $A = PDP^{-1}$，则称 $A$ 可对角化.

定理 5 $\quad$ (对角化定理)

$n \times n$ 矩阵 $A$ 可对角化的充分必要条件是 $A$ 有 $n$ 个线性无关的特征向量.

事实上，$A=PDP^{-1}$，$D$ 为对角矩阵的充分必要条件是 $P$ 的列向量是 $A$ 的 $n$ 个线性无关的特征向量. 此时，$D$ 的主对角线上的元素分别是 $A$ 的对应于 $P$ 中特征向量的特征值.

换句话说，$A$ 可对角化的充分必要条件是有足够的特征向量形成 $\Bbb R^n$ 的基，我们称这样的基为特征向量基.

矩阵的对角化

一、 求出 $A$ 的特征值 (利用特征方程 $\det(A-\lambda I)=0$).

二、 求 $A$ 的 $n$ 个线性无关的特征向量 (利用 $(A-\lambda I)\mathbf{x}=0$ 求出特征空间的基).

三、 用第2步得到的特征向量构造可逆矩阵 $P$.

四、 用对应的特征值构造对角矩阵 $D$.

定理 6 $\quad$ 有 $n$ 个特征值的 $n \times n$ 矩阵可对角化.

特征值不是都相异的矩阵

定理 7 $\quad$ 设 $A$ 是 $n \times n$ 矩阵，其相异的特征值是 $\lambda_1,\cdots,\lambda_p$.

1. 对于 $1 \le k \le p$，$\lambda_k$ 的特征空间的维数小于或等于 $\lambda_k$ 的代数重数.
2. 矩阵 $A$ 可对角化的充分必要条件是所有不同特征空间的维数之和为 $n$. 即每个 $\lambda_k$ 的特征空间的维数等于 $\lambda_k$ 的代数重数.
3. 若 $A$ 可对角化，$\mathcal{B}_k$ 是对应于 $\lambda_k$ 的特征空间的基，那么，集合 $\mathcal{B}_1,\cdots,\mathcal{B}_p$ 中所有向量的集合是 $\Bbb R^n$ 的特征向量基.

5.4 特征向量与线性变换

线性变换的矩阵

设 $V$ 是 $n$ 维向量空间，$W$ 是 $m$ 维向量空间，$T$ 是 $V$ 到 $W$ 的线性变换. 为了把 $T$ 与矩阵相联系，我们指定 $\mathcal{B}$ 和 $\mathcal{C}$ 分别是 $V$ 和 $W$ 的基.

若 $\mathbf{x} \in V$，坐标向量 $[\mathbf{x}]_{\mathcal{B}} \in \Bbb R^n$，$\mathbf{x}$ 的像 $T(\mathbf{x})$ 的坐标向量 $[T(\mathbf{x})]_{\mathcal{C}} \in \Bbb R^m$. 设 $V$ 的基 $\mathcal{B}$ 是 $\{\mathbf{b_1,\cdots,b_n}\}$，若 $\mathbf{x} = r_1\mathbf{b_1}+\cdots+r_n\mathbf{b_n}$，则

\[[\mathbf{x}]_{\mathcal{B}} = \begin{bmatrix} r_1 \\ \vdots \\ r_n \end{bmatrix}\]

因为 $T$ 是线性的，故

\[T(\mathbf{x}) = T(r_1\mathbf{b_1}+\cdots+r_n\mathbf{b_n}) = r_1T(\mathbf{b_1}) + \cdots + r_nT(\mathbf{b_n}) \tag{5.1}\label{eq5.1}\]

利用 $W$ 的基 $\mathcal{C}$，可以用 $\mathcal{C}$-坐标向量来改写 \eqref{eq5.1}

\[[T(\mathbf{x})]_{\mathcal{C}} = r_1[T(\mathbf{b_1})]_{\mathcal{C}} + \cdots + r_n[T(\mathbf{b_n})]_{\mathcal{C}} \tag{5.2}\label{eq5.2}\]

向量等式 \eqref{eq5.2} 可以写为矩阵等式

\[[T(\mathbf{x})]_{\mathcal{C}} = M[\mathbf{x}]_{\mathcal{B}} \tag{5.3}\label{eq5.3}\]

其中

\[M = [[T(\color{#a8f}{\mathbf{b_1}})]_{\color{#f0f}{\mathcal{C}}} \quad [T(\color{#a8f}{\mathbf{b_2}})]_{\color{#f0f}{\mathcal{C}}} \quad \cdots \quad [T(\color{#a8f}{\mathbf{b_n}})]_{\color{#f0f}{\mathcal{C}}}] \tag{5.4}\label{eq5.4}\]

矩阵 $M$ 是 $T$ 的矩阵表示，称为 $T$ 相对于基 $\color{#a8f}{\mathcal{B}}$ 和 $\color{#f0f}{\mathcal{C}}$ 的矩阵.

\[\require{AMScd} \begin{CD} \mathbf{x} @>{T}>> T(\mathbf{x}) \\ @VVV @VVV \\ [\mathbf{x}]_{\mathcal{B}} @>{乘以M}>> [T(\mathbf{x})]_{\mathcal{C}} \end{CD}\]

$V$ 到 $V$ 的线性变换

当 $W=V, \mathcal{C}=\mathcal{B}$时，\eqref{eq5.4} 中的 $M$ 称为 $T相对于\mathcal{B}的矩阵$，或简称为 $T的\mathcal{B}-矩阵$，记为 $[T]_{\mathcal{B}}$.

\[\require{AMScd} \begin{CD} \mathbf{x} @>T>> T(\mathbf{x}) \\ @VVV @VVV \\ [\mathbf{x}]_{\mathcal{B}} @>{乘以[T]_{\mathcal{B}}}>> [T(\mathbf{x})]_{\mathcal{B}} \end{CD}\]

$V \to V$ 的线性变换 $T$ 的 $\mathcal{B}$-矩阵对所有 $V$ 中的 $\mathbf{x}$，有

\[[T(\mathbf{x})]_{\mathcal{B}} = [T]_{\mathcal{B}}[\mathbf{x}]_{\mathcal{B}} \tag{5.5}\label{eq5.5}\]

$\Bbb R^n$ 上的线性变换

定理 8 $\quad$ (对角矩阵表示)

设 $A=PDP^{-1}$，其中 $D$ 为 $n \times n$ 对角矩阵，若 $\Bbb R^n$ 的基 $\mathcal{B}$ 由 $P$ 的列向量组成，那么 $D$ 是变换 $\mathbf{x} \mapsto A\mathbf{x}$ 的 $\mathcal{B}$-矩阵.

记 $P$ 的列向量为 $\mathbf{b_1,\cdots,b_n}$，则有 $\mathcal{B}=\{\mathbf{b_1,\cdots,b_n}\},P=[b_1\;\cdots\;b_n]$. 因此，$P$ 是坐标变换矩阵 $P_{\mathcal{B}}$

\[\mathbf{x} = P[\mathbf{x}]_{\mathcal{B}} 和 [\mathbf{x}]_{\mathcal{B}}=P^{-1}\mathbf{x}\]

若 $\mathbf{x} \in \Bbb R^n, T(\mathbf{x})=A\mathbf{x}$，那么

\[\begin{aligned} [T]_{\mathcal{B}} &= [[T(\mathbf{b_1})]_{\mathcal{B}}\quad\cdots\quad[T(\mathbf{b_n})]_{\mathcal{B}}] & 由[T]_{\mathcal{B}}定义 \\ &= [[A\mathbf{b_1}]_{\mathcal{B}}\quad\cdots\quad[A\mathbf{b_n}]_{\mathcal{B}}] & 由T(\mathbf{x})=A\mathbf{x} \\ &= [P^{-1}A\mathbf{b_1}\quad\cdots\quad P^{-1}A\mathbf{b_n}] & 坐标变换 \\ &= P^{-1}A[\mathbf{b_1}\quad\cdots\quad\mathbf{b_n}] & 矩阵乘法 \\ &= P^{-1}AP \\ &= D & 相似性P^{-1}AP=D \end{aligned}\]

矩阵表示的相似性

若 $A$ 相似于 $C$，即有 $A=PCP^{-1}$，如果 $\mathcal{B}$ 由 $P$ 的列向量组成，则 $C$ 是变换 $\mathbf{x} \mapsto A\mathbf{x}$ 的 $\mathcal{B}$-矩阵.

\[\require{AMScd} \begin{CD} \mathbf{x} @>{乘以A}>> A\mathbf{x} \\ @V{乘以P^{-1}}VV @AA{乘以P}A \\ [\mathbf{x}]_{\mathcal{B}} @>>{乘以C}> [A\mathbf{x}]_{\mathcal{B}} \end{CD}\]

六、正交性和最小二乘法

6.1 内积、长度和正交性

内积

如果 $\mathbf{u}$ 和 $\mathbf{v}$ 是 $\Bbb R^n$ 空间中的向量，可以将 $\mathbf{u}$ 和 $\mathbf{v}$ 作为 $n \times 1$ 矩阵. 向量 $\mathbf{u}^T$ 是 $1 \times n$ 矩阵且矩阵乘积 $\mathbf{u}^T\mathbf{v}$ 是一个 $1 \times 1$ 矩阵，我们将其记为一个不加括号的实数. $\mathbf{u}^T\mathbf{v}$ 称为 $\mathbf{u}$ 和 $\mathbf{v}$ 的内积，记作 $\mathbf{u}\cdot\mathbf{v}$. 内积也称为点积. 如果

\[\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \qquad \mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\]

那么 $\mathbf{u}$ 和 $\mathbf{v}$ 的内积为

\[\mathbf{u} \cdot \mathbf{v} = \mathbf{u}^T\mathbf{v} = [u_1 \quad u_2 \quad \cdots u_n] \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]

定理 1 $\quad$ 设 $\mathbf{u,v,w}$ 是 $\Bbb R^n$ 空间中的向量，$c$ 是一个数，那么

1. $\mathbf{u}\cdot\mathbf{v} = \mathbf{v}\cdot\mathbf{u}$
2. $(\mathbf{u+v})\cdot\mathbf{w} = \mathbf{u}\cdot\mathbf{w} + \mathbf{v}\cdot\mathbf{w}$
3. $(c\mathbf{u})\cdot\mathbf{v} = c(\mathbf{u}\cdot\mathbf{v}) = \mathbf{u}(c\cdot\mathbf{v})$
4. $\mathbf{u}\cdot\mathbf{u} \ge 0$，并且 $\mathbf{u}\cdot\mathbf{u}=0$ 成立的充分必要条件是 $\mathbf{u}=\mathbf{0}$

向量的长度

定义 $\quad$ 向量 $\mathbf{v}$ 的长度 (范数) 是非负数 $\|\mathbf{v}\|$，定义为

\[\|\mathbf{v}\| = \sqrt{\mathbf{v}\cdot\mathbf{v}} = \sqrt{v_1^2+v_2^2+\cdots+v_n^2}，且 \|\mathbf{v}\|^2 = \mathbf{v}\cdot\mathbf{v}\]

长度为 $1$ 的向量称为单位向量，如果把一个非零向量除以自身的长度，即乘 $\dfrac{1}{\|\mathbf{v}\|}$，就可以得到一个单位化的向量 $\mathbf{u}=\dfrac{\mathbf{v}}{\|\mathbf{v}\|}$. 这种把向量 $\mathbf{v}$ 化为单位向量 $\mathbf{u}$ 的过程，称为向量 $\mathbf{v}$ 的单位化，且此时 $\mathbf{u}$ 和 $\mathbf{v}$ 方向一致.

$\Bbb R^n$ 空间中的距离

定义 $\quad$ $\Bbb R^n$ 中向量 $\mathbf{u}$ 和 $\mathbf{v}$ 的距离，记作 $\mathrm{dist}(\mathbf{u},\mathbf{v})$，表示向量 $\mathbf{u-v}$ 的长度，即

\[\mathrm{dist}(\mathbf{u},\mathbf{v}) = \|\mathbf{u-v}\|\]

正交向量

正交是线性代数中的一个通用术语，表示 $\Bbb R^n$ 空间中两个向量相互垂直.

定义 $\quad$ 如果 $\mathbf{u}\cdot\mathbf{v}=0$，则两个向量 $\mathbf{u}$ 和 $\mathbf{v}$ 称为 (相互) 正交的.

由 $\mathbf{0}^T\cdot\mathbf{v}=0$ 对任意 $\mathbf{v}$ 都成立，可以得出零向量与任意向量正交.

定理 2 $\quad$ (毕达哥拉斯 (勾股) 定理)

两个向量 $\mathbf{u}$ 和 $\mathbf{v}$ 正交的充分必要条件是 $\|\mathbf{u+v}\|^2 = \|\mathbf{u}\|^2 + \|\mathbf{v}\|^2$.

正交补

如果向量 $\mathbf{z}$ 与 $\Bbb R^n$ 的子空间 $W$ 中的任意向量都正交，则称 $\mathbf{z}$ 正交于 $W$. 与子空间 $W$ 正交的向量 $\mathbf{z}$ 的全体组成的集合称为 $W$ 的正交补，并记作 $W^{\bot}$ ($W^{\bot}$ 读作 $W$ 的正交补).

两个关于 $W^{\bot}$ 的性质:

1. 向量 $\mathbf{x}$ 属于 $W^{\bot}$ 的充分必要条件是向量 $\mathbf{x}$ 与生成空间 $W$ 的任一向量都正交.
2. $W^{\bot}$ 是 $\Bbb R^n$ 的一个子空间.

定理 3 $\quad$ 假设 $A$ 是 $m \times n$ 矩阵，那么 $A$ 的行向量空间的正交补空间是 $A$ 的零空间，且 $A$ 的列向量空间的正交补是 $A^T$ 的零空间:

\[(\mathrm{Row}A)^{\bot} = \mathrm{Nul}A 且 (\mathrm{Col}A)^{\bot} = \mathrm{Nul}A^T\]

$\Bbb R^2$ 空间和 $\Bbb R^3$ 空间的角度

如果 $\mathbf{u}$ 和 $\mathbf{v}$ 是 $\Bbb R^2$ 或 $\Bbb R^3$ 中的非零向量，那么可以用内积，将从原点到点 $\mathbf{u}$ 和原点到点 $\mathbf{v}$ 的两个线段之间的夹角联系起来，对应的公式是:

\[\mathbf{u}\cdot\mathbf{v} = \|\mathbf{u}\|\|\mathbf{v}\|\cos\theta\]

6.2 正交集

有 $\Bbb R^n$ 中的向量集合 $\{\mathbf{u_1,\cdots,u_p}\}$，如果集合中任意两个不同向量都正交，即当 $i \ne j$ 时，$u_i \cdot u_j = 0$，则该集合称为正交向量集.

定理 4 $\quad$ 如果 $S=\{\mathbf{u_1,\cdots,u_p}\}$ 是由 $\Bbb R^n$ 空间中非零向量构成的正交集，那么 $S$ 是线性无关集，因此构成所生成的子空间 $S$ 的一组基.

定义 $\quad$ $\Bbb R^n$ 中子空间 $W$ 的一个正交基是 $W$ 的一个基，且是正交集.

定理 5 $\quad$ 假设 $\{\mathbf{u_1,\cdots,u_p}\}$ 是 $\Bbb R^n$ 中子空间 $W$ 的正交基，对 $W$ 中的每个向量 $\mathbf{y}$，线性组合 $\mathbf{y}=c_1\mathbf{u_1}+\cdots+c_p\mathbf{u_p}$ 中的权值可以由 $c_j = \dfrac{\mathbf{y\cdot u_j}}{\mathbf{u_j}\cdot\mathbf{u_j}}\;(j=1,\cdots,p)$ 计算.

因此线性组合 $\mathbf{y}=c_1\mathbf{u_1}+\cdots+c_p\mathbf{u_p}$ 可以表示为 $\mathbf{y}=\dfrac{\mathbf{y \cdot u_1}}{\mathbf{u_1 \cdot u_1}}\mathbf{u_1}+\cdots+\dfrac{\mathbf{y \cdot u_p}}{\mathbf{u_p \cdot u_p}}\mathbf{u_p}$

单位正交集

由单位向量构成的正交集 $\{\mathbf{u_1,\cdots,u_p}\}$ 是一个单位正交集. 如果 $W$ 是一个由单位正交集生成的子空间，那么 $\{\mathbf{u_1,\cdots,u_p}\}$ 是 $W$ 的单位正交基.

正交集中向量被”单位化”后，具有单位长度，集合中新向量的正交性不变，因此新的集合成为单位正交基.

各列形成单位正交基的矩阵，在矩阵算法和计算中都非常重要，其性质由下面定理 6和定理 7给出.

定理 6 $\quad$ 一个 $m \times n$ 矩阵 $U$ 具有单位正交列向量的充分必要条件是 $U^TU=I$.

定理 7 $\quad$ 假设 $U$ 是一个具有单位正交列的 $m \times n$ 矩阵，且 $\mathbf{x}$ 和 $\mathbf{y}$ 是 $\Bbb R^n$ 的向量，那么

1. $\|U\mathbf{x}\|=\|\mathbf{x}\|$.
2. $(U\mathbf{x})\cdot(U\mathbf{y})=\mathbf{x}\cdot\mathbf{y}$.
3. $(U\mathbf{x})\cdot(U\mathbf{y})=0$ 的充分必要条件是 $\mathbf{x}\cdot\mathbf{y}=0$.

一个正交矩阵就是一个可逆的方阵 $U$，且满足 $U^{-1}=U^T$，由定理6，这样的矩阵具有单位正交列。任何单位正交的方阵是正交矩阵.