计数法 (Counting Methods)
计数法则基于分阶段计数的原则。
乘法法则 (Multiplication Rule)
假设一个试验有 $k$ 个部分 ($k \geq 2$):
- 试验的第 $i$ 部分可以有 $n_i$ 个可能的结果 ($i=1,\dots,k$);
- 每个部分中的所有结果都可以发生,并且不依赖于其它部分的结果;
- 试验的样本空间 $S$ 将包含形式为 ($u_1,\dots,u_k$) 的所有向量,其中 $u_i$ 是第 $i$ 部分 ($i=1,\dots,k$) 的 $n_i$ 个可能结果之一。
- 这些向量在 $S$ 中的总数等于 $n_1 n_2 \cdots n_k$ 的乘积。
例:含有 $n$ 个元素的集合,子集的个数是多少?
根据已知有限集构造一个子集,该子集对于每一个元素,要么包含要么不包含,根据乘法法则,这个子集共有 $\underbrace{2 \times 2 \times \cdots \times 2}_n$ 种构造方式,即有 $2^n$ 个子集。
排列 (Permutations)
$n$ 选 $k$ 排列
假设一个集合中有 $n$ 个不同的对象:
- 第 $1$ 阶段,从 $n$ 个对象中选出一个
- 第 $2$ 阶段,从剩下的 $n-1$ 个对象中选出一个
$\vdots$ - 第 $k$ 阶段,从剩下的 $n-(k-1)$ 个对象中选出一个
根据乘法法则,一共会有
\[n(n-1)\cdots(n-k+1)\]种可能的排列,记作: $P_{n,k}$。
当 $k=n$ 时,有:
\[P_{n,n} = n(n-1)\cdots 1 = n!\]符号 $n!$ 读作 $n$ 的阶乘。此时,$P_{n,k}$ 可以被重写为:
\[P_{n,k} = n(n-1)\cdots(n-k+1)\frac{(n-k)\cdots 2 \cdot 1}{(n-k)\cdots 2 \cdot 1} = \frac{n!}{(n-k)!}\]组合 (Combinations)
考虑具有 $n$ 个元素的集合,从这个集合中取出含有 $k$ 个元素的每个子集,称为从 $n$ 中取 $k$ 的组合,记作: $C_{n,k}$。
组合中的 $k$ 个元素是没有顺序的,任何两个包含相同元素的子集都被认为是同一个子集。含有 $k$ 个元素的子集对应了 $k!$ 个不同的排列。我们可以考虑将 $n$ 选 $k$ 排列分成两部分,第一部分,是一个从 $n$ 中取出 $k$ 个元素的组合,第二部分,是这 $k$ 个元素的一个排列,因为有 $C_{n,k}$ 种组合,每个组合有 $k!$ 种排列,使用乘法法则,可以得到 $P_{n,k} = C_{n,k} \cdot k!$。因此,从 $n$ 中取 $k$ 的组合数为,
\[C_{n,k} = \frac{P_{n,k}}{k!} = \frac{n!}{k!(n-k)!}\]条件概率 (Conditional probability)
设事件 $B$ 满足 $\mathrm{P}(B) \gt 0$,则给定 $B$ 之下,事件 $A$ 的条件概率为
\[\mathrm{P}(A) = \frac{\mathrm{P}(A\cap B)}{\mathrm{P}(B)}\]乘法规则
假定所有涉及的条件概率都是正的,那么事件 $A_1\cap A_2\cap \cdots \cap A_n$ 的概率为
\[\begin{aligned} \mathrm{P}(\cap_{i=1}^nA_i) &= \mathrm{P}(A_1\cap A_2\cap \cdots \cap A_n) \\ &= \mathrm{P}(A_1)\cdot\mathrm{P}(A_2\vert A_1)\cdot\mathrm{P}(A_3\vert A_1\cap A_2)\cdot\;\cdots\;\cdot\mathrm{P}(A_n\vert A_1\cap A_2\cap\cdots\cap A_{n-1}) \end{aligned}\]全概率公式
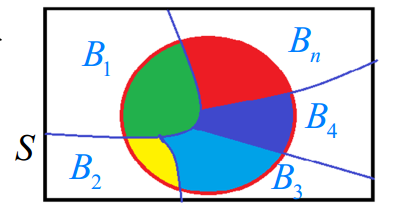
设 $B_1,B_2,\cdots,B_n$ 是一组互不相容事件,形成样本空间的一个分割(每个试验结果必定使得其中一个事件发生)。又假定对每一个 $i, \mathrm{P}(B)>0$,则对于任意事件 $A$,下列公式成立
\[\begin{aligned} \mathrm{P}(A) &= \sum_{i=1}^n \mathrm{P}(A\cap B_i) \\[2ex] &= \mathrm{P}(A\cap B_1) + \cdots + \mathrm{P}(A\cap B_n) \end{aligned}\]又因为条件概率
\[\mathrm{P}(A\cap B_i) = \mathrm{P}(B_i)\mathrm{P}(A\cap B_i)\]全概率公式又可写作
\[\begin{aligned} \mathrm{P}(A) &= \sum_{i=1}^n \mathrm{P}(B_i) \mathrm{P}(A\vert B_i) \\[2ex] &= \mathrm{P}(B_1)\mathrm{P}(A\vert B_1) + \cdots + \mathrm{P}(B_n)\mathrm{P}(A\vert B_n) \end{aligned}\]全概率公式将对一复杂事件 $A$ 的概率求解,转化为了在不同原因 $B_i$ 下发生的简单事件的概率求和问题。
随机变量 (Random variable)
样本空间和事件
- 每个概率模型都关联着一个试验,这个试验将产生一个试验结果,该试验所有可能的结果形成样本空间,用 $\Omega$ 表示样本空间。
- 样本空间的子集,即某些试验结果的集合,称为随机事件,简称事件。在一次试验中,当且仅当这个子集中的一个试验结果出现,就称这一事件发生。
- 只含一个试验结果的集合称为基本事件,整个样本空间 $\Omega$ 称为必然事件,不包含任何试验结果的空集称为不可能事件。
- 在确定样本空间的时候,不同的试验结果必须是相互排斥的。
概率空间三要素 $(\Omega, \mathcal{F}, \Bbb{P})$
知乎 - 怎样理解概率空间这个概念和概率空间的三要素(Ω,F,P)?
-
$\Omega$ - Sample space 样本空间,试验中所有可能结果的集合。(注:每个结果需要互斥,所有可能结果必须被穷举)
-
$\mathcal{F}$ - Set of events 事件集合。是 $\Omega$ 的一些子集构成的集合。$\mathcal{F}$ 中的元素称为事件。
-
$\Bbb{P}$ - Probability measure 概率测度或概率。$\Bbb{P}$ 是一个定义在 $\mathcal{F}$ 的函数,是一个集合的函数,它的自变量是集合,称为概率。
随机变量 (Random variable)
一个随机试验的可能结果(称为基本事件)的全体组成一个基本空间 $\Omega$。随机变量 $X$ 是定义于 $\Omega$ 上的函数 $X: \Omega \to \Bbb{R}$,即对 每一基本事件 $\omega \in \Omega$ ,有一数值 $X(\omega)$ 与之对应。
对于样本空间 $\Omega$ 中的样本 $\omega$,可以取各种不同的映射,得到不同的随机变量。
事件 $\{X=x\}$ 表示试验结果 $\{\omega : X(\omega)=x\}$ 的集合。
随机变量 $X$ 的每一个取值,对应着一个不同的事件,如:$\{X=1\}$ 对应事件 $A$,$\{X=0\}$ 对应事件 $B$ 等。
概率分布 (Probability distribution)
随机变量 $X$ 的概率分布计算
对每一个随机变量 $X$ 的值 $x$:
- 找出与事件 $\{X=x\}$ 相对应的所有试验结果 $\{\omega:X(\omega) = x\}$;
- 将这些试验结果的概率相加得到 $p_X(x)$
因此,事件 $\{X=x\}$ 的概率为
\[p_X(x)=P(\{X=x\})=P(\{\omega:X(\omega)=x\})\]常见随机变量概率分布
伯努利随机变量概率分布 (Bernoulli distribution)
随机变量
\[X(\omega) = \left\{ \begin{aligned} 1 & \quad \text{正面朝上}\\ 0 & \quad \text{正面朝下} \end{aligned} \right.\]概率分布
\[p_X(k) = \left\{ \begin{aligned} & p & (k=0) \\ & 1-p & (k=1) \end{aligned} \right.\]离散均匀随机变量概率分布 (Uniform distribution)
\[p_X(k) = \left\{ \begin{aligned} & \frac{1}{b-a+1} &\quad &(k=a,a+1,\cdots,b) \\ & 0 &\quad &\text{其它} \end{aligned} \right.\]二项随机变量概率分布 (Binomial distribution)
\[p_X(k) = P(X=k) = \binom{n}{k}p^k(1-p)^{n-k} \quad (k=0,1,\dots,n)\]几何随机变量概率分布 (Geometric distribution)
\[p_X(k)=(1-p)^{k-1}p \quad (k=1,2,\dots)\]泊松随机变量概率分布 (Poisson distribution)
\[p_X(k)=e^{-\lambda}\frac{\lambda^k}{k!} \quad (k=0,1,2,\dots)\]随机变量的函数
\[Y = g(X) = \left\{ \begin{aligned} aX + b & \quad \text{(线性函数)} \\ \log(X) & \quad \text{(非线性函数)} \end{aligned} \right.\]随机变量的函数 $\{Y=y\}$ 的概率是所有函数取值为 $y$ 的随机变量 $\{x \vert g(x)=y\}$ 的概率之和。
\[P_Y(y) = \sum_{\{x|g(x)=y\}} p_X(x)\]随机变量的期望 (Expected value)
随机变量 $X$ 的期望 $\mathrm{E}[X]$(也可以称为均值,用符号 $\mu$ 表示)
\[\mathrm{E}[X] = \left\{ \begin{aligned} & \sum_x xp_X(x) &\; (离散随机变量) \\[2ex] & \int_{-\infty}^{\infty}xf_X(x)\mathrm{d}x &\; (连续随机变量) \end{aligned} \right.\]随机变量的函数的期望
\[\mathrm{E}[g(X)] = \left\{ \begin{aligned} & \sum_x g(x)p_X(x) &\; (离散随机变量) \\[2ex] & \int_{-\infty}^{\infty}g(x)f_X(x)\mathrm{d}x &\; (连续随机变量) \end{aligned} \right.\]随机变量 $X$ 的 $n$ 阶矩
\[\mathrm{E}[X^n] = \left\{ \begin{aligned} & \sum_x x^np_X(x) &\; (离散随机变量) \\[2ex] & \int_{-\infty}^{\infty}x^nf_X(x)\mathrm{d}x &\; (连续随机变量) \end{aligned} \right.\]随机变量的方差和标准差 (Variance and Standard deviation)
方差和标准差提供了随机变量 $X$ 在其期望周围分散程度的一个测度。
随机变量 $X$ 的方差
\[\begin{aligned} \mathrm{var}(X) &= \mathrm{E}\left[(X-\mathrm{E}[X])^2\right] \\[2ex] \mathrm{var}(X) &= \left\{ \begin{aligned} & \sum_x(x-\mathrm{E}[X])^2 p_X(x) &\; (离散随机变量) \\[2ex] & \int_{-\infty}^{\infty}(x-\mathrm{E}[X])^2f_X(x)\mathrm{d}x &\; (连续随机变量) \end{aligned} \right. \\ \mathrm{var}(X) &= \mathrm{E}[X^2] - (\mathrm{E}[X])^2 \end{aligned}\]随机变量 $X$ 的标准差
\[\sigma_X = \sqrt{\mathrm{var}(X)}\]标准差的量纲与 $X$ 相同,因此具有可比性。
随机变量线性函数的均值和方差
设 $X$ 为随机变量,令
\[Y = aX+b\]其中 $a$ 和 $b$ 为给定常数,则
\[\mathrm{E}[Y]=a\mathrm{E}[X]+b, \quad \mathrm{var}(Y)=a^2\mathrm{var}(X)\]常见随机变量的均值与方差
伯努利随机变量的均值与方差
\[\begin{aligned} \mathrm{E}[X] &= 1\cdot p + 0\cdot(1-p) = p \\ \mathrm{E}[X^2] &= 1^2\cdot p + 0^2\cdot(1-p) = p \\ \mathrm{var}(X) &= \mathrm{E}[X^2] - (\mathrm{E}[X])^2 = p - p^2 = p(1-p) \end{aligned}\]离散均匀随机变量的均值与方差
\[\begin{aligned} \mathrm{E}[X] &= \frac{a+b}{2} \\ \mathrm{var}(X) &= \frac{(b-a)(b-a+2)}{12} \end{aligned}\]多随机变量的联合分布 (Joint probability distribution)
在同一个试验中有两个随机变量 $X$ 和 $Y$,它们的取值概率由 联合分布 来描述,并且用 $p_{X,Y}$ 表示。
\[\begin{aligned} p_{X,Y}(x,y) &= \mathrm{P}(\{X=x\}\cap \{Y=y\}) \\ &= \mathrm{P}(X=x,Y=y) \end{aligned}\]假设事件 $A=\{X=x\}$,事件 $B=\{Y=y\}$,那么 $\mathrm{P}(A\cap B)$ 相当于 $p_{X,Y}(x,y)$
可以利用 $X$ 和 $Y$ 联合分布来计算 $X$ 或 $Y$ 的边缘分布
\[\begin{aligned} p_X(x) &= \sum_y p_{X,Y}(x,y) \\ p_Y(y) &= \sum_x p_{X,Y}(x,y) \end{aligned}\]