微分
切线(tangent line)是数学中的一个基本概念,通常用于函数图形或几何图形,切线的基本定义:
- 在几何学中,圆的切线被定义为与圆只有一个公共点(切点)的直线。这是切线最直观的定义,可以扩展到其他几何图形,比如椭圆或多边形。
- 在微积分中,一条切线是曲线在某一特定点上的 直线近似。更严谨地说,若曲线为函数 $y = f(x)$,那么在点 $(a, f(a))$ 处的切线,设为 $y=L(x)$,是该点的唯一一条直线,其斜率(slope)等于函数在该点的导数 $f’(a)$。这条直线 $L(x)$ 与曲线 $f(x)$ 在 $x=a$ 处通过直线的斜率 $m$ 和曲线的导数 $f’(a)$ 联系在一起,换句话说,这条直线在点 $(a, f(a))$ 附近与函数 $y = f(x)$ 的图形非常接近,斜率 $m$ 为
给定斜率后,可以使用点斜式等式来描述这条直线:
\[y - f(a) = f'(a)(x - a)\]切线的概念是分析和理解函数局部行为非常有用的工具,它是微积分中研究变化率和做线性近似的基础。
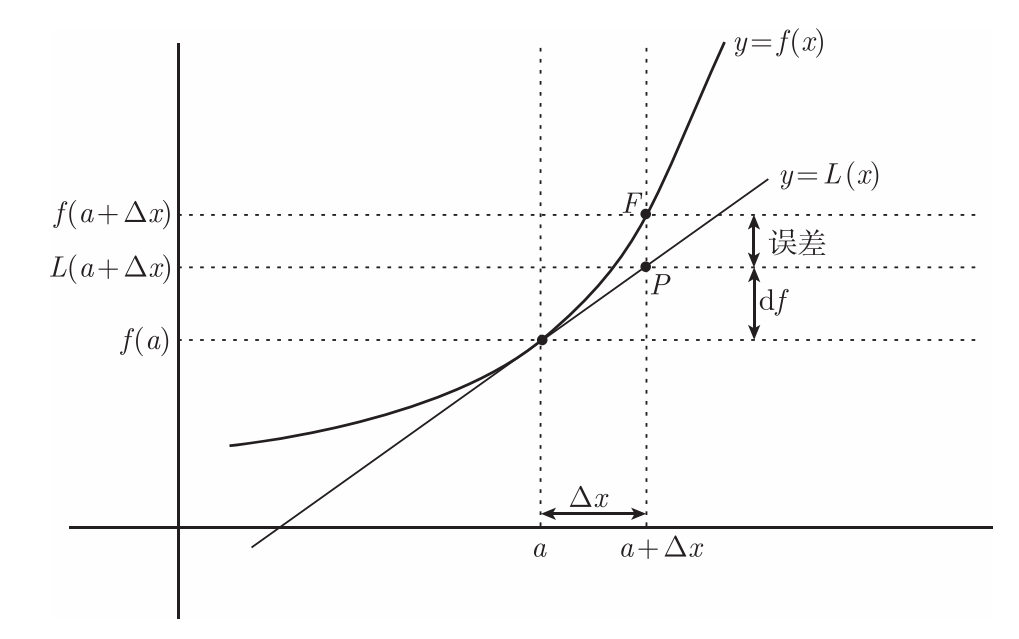
这个线性函数 $L$ 被称为 $f$ 在 $x = a$ 处的 线性化。在上图中, 还有个量被标记了出来, 那就是 $\mathrm{d}f$, 也就是点 $P$ 和 $f(a)$ 的高度之差,可以通过在点 $a$ 处的斜率及 $x$ 的变化量得到
\[\boxed{\mathrm{d}f = f'(a)\Delta x}\]量 $\mathrm{d}f$ 被称为 $f$ 在 $x=a$ 处的 微分。它是对当 $x$ 从 $a$ 变化为 $a+\Delta x$ 时 $f$ 的变化量的近似。
伸缩级数
\[\boxed{\sum_{j=a}^b(f(j)-f(j-1)) = f(b)-f(a-1)}\]伸缩级数 只需要考虑级数展开后两个端点的值和对应符号,因为中间部分的各项会被消掉。例如 $f(j) = j^2$:
展开后的两个端点分别为 $-0^2$ 和 $+5^2$,因此消掉中间项后就等于 $5^2-0^2$。考虑下面的公式,
\[\sum_{j=1}^n(j^2-(j-1)^2) = n^2 - (1-1)^2 = n^2\]而 $j^2-(j-1)^2 = j^2 - (j^2-2j+1) = 2j-1$, 因此
\[\boxed{\sum_{j=1}^n(2j-1)=n^2}\]这就是 奇数和公式。然后再对公式进行整理,
因此,
\[\boxed{\sum_{j=1}^n j = \frac{n(n+1)}{2}}\]就是 n项和公式。同样,对于 $f(j)= j^3$,有
将 $j^3-(j-1)^3$ 展开后得到 $3j^2-3j+1$,代入上式整理后可得 平方和公式,
反常积分与无穷级数
对于积分 $\int_a^bf(x)\,\mathrm{d}x$,如果在区间 $[a,b]$ 有一条垂直渐近线,被积函数 $f$ 在渐近线附近变得很大,且没有界限,则该积分变成反常积分。另外,如果积分区间是无界的,如 $[0,\infty]、[-\infty,3]、(-\infty, \infty)$,也会使积分变为反常积分。
以下几种情况,会使积分 $\int_a^bf(x)\,\mathrm{d}x$ 变为反常积分:
- 函数 $f$ 在闭区间 $[a,b]$ 内是无界的;
- $b=\infty$
- $a=-\infty$
数列与函数的关系
数列 $a_n$ 可以认为是定义域为自然数集 $\Bbb N$ 的函数 $f:n \to a_n,\;(n \in \Bbb N)$,即
\[a_n = f(n), \quad (n \in \Bbb N)\]反常积分与无穷级数的关系
| 名称 | 公式 | 名称 | 公式 |
|---|---|---|---|
| 数列 | $\{a_n\}$ | 函数 | $f(x)$ |
| 无穷级数 | $\sum\limits_{n=1}^\infty a_n$ | 在 $\int^\infty$ 处的反常积分 | $\int_a^\infty f(x)\,\mathrm{d}x$ |
| 部分和数列 | $\left\{\sum\limits_{n=1}^N a_n\right\}$ | 定积分 | $\int_a^N f(x)\,\mathrm{d}x$ |
| 无穷级数极限定义 | $\sum\limits_{n=1}^\infty a_n = \lim\limits_{N \to \infty}\sum\limits_{n=1}^N a_n$ | 在 $\int^\infty$ 处的反常积分极限定义 | $\int_a^\infty f(x)\,\mathrm{d}x = \lim\limits_{N \to \infty}\int_a^N f(x)\,\mathrm{d}x$ |
反常积分的收敛与发散
1. 比较判别法
如果在区间 $(a,b)$ 内,函数 $f(x) \ge g(x) \ge 0$,且积分 $\int_a^b g(x)\,\mathrm{d}x$ 是发散的,那么积分 $\int_a^b f(x)\, \mathrm{d}x$ 也是发散的。数学形式为:
\[\int_a^b f(x)\,\mathrm{d}x \ge \int_a^b g(x)\,\mathrm{d}x = \infty\]如果在区间 $(a,b)$ 内,函数 $0 \le f(x) \le g(x)$,且积分 $\int_a^b g(x)\,\mathrm{d}x$ 是收敛的,那么积分 $\int_a^b f(x)\, \mathrm{d}x$ 也是收敛的。数学形式为:
\[\int_a^b f(x)\,\mathrm{d}x \le \int_a^b g(x)\,\mathrm{d}x \lt \infty\]2. 极限比较判别法
假设有函数 $f(x)$ 和 $g(x)$ 在破裂点 $x=a$ 处非常接近(没有其他破裂点),那么积分 $\int_a^b f(x)\,\mathrm{d}x$ 和 $\int_a^b g(x)\,\mathrm{d}x$ 同时收敛或同时发散,它们的行为相同。数学形式为:
\[当 x \to a时, f(x) \sim g(x)等同于\lim_{x \to a}\frac{f(x)}{g(x)}=1\]上式表示,当 $x \to a$ 时,$f(x)$ 与 $g(x)$ 渐近等价。渐近等价有以下几种方式:
-
渐近等价的函数同时做幂运算。如:
当 $x \to 0$ 时有 $\sin(x) \sim x$,则有 $x \to 0$ 时 $\sin^3(x) \sim x^3$。 -
用其它趋于 $0$ 的量替代 $x$。如:
当 $x \to 0$ 时有 $\sin(x) \sim x$,则有 $x \to 0$ 时 $\sin(4x^7) \sim 4x^7$。 -
两个渐近等价的函数相乘或相除。如:
当 $x \to 0$ 时有 $\sin(x) \sim x$ 和 $\tan(x) \sim x$,则有 $x \to 0$ 时 $\tan(x)\sin(x) \sim x^2$。
注意: 两个渐近等价的函数不能相加或相减。
3. $p$ 判别法
使用比较判别法和极限比较判别法时,需要选取一个合适的函数 $g(x)$,该函数足够简单,可以判断是收敛的还是发散的。最常用的函数是 $\dfrac{1}{x^p}$,其中 $p \gt 0$。例如:函数 $\dfrac{1}{\sqrt x}、\dfrac{1}{x}$ 和 $\dfrac{1}{x^2}$,分别对应于 $p=\dfrac{1}{2}、1$ 和 $2$。对于积分
\[\int_a^\infty \dfrac{1}{x^p}\,\mathrm{d}x \quad 和 \quad \int_0^a \dfrac{1}{x^p}\,\mathrm{d}x\]-
$p$ 判别法,$\int^\infty$ 的情况:对于任何有限值 $a \gt 0$,当 $p \gt 1$ 时收敛,$p \le 1$ 时发散。
-
$p$ 判别法,$\int_0\;\;$ 的情况:对于任何有限值 $a \gt 0$,当 $p \lt 1$ 时收敛,$p \ge 1$ 时发散。
注意到当 $p=1$ 时,对应 $\dfrac{1}{x}$,在上面两种积分中都是发散的。
4. 绝对收敛判别法
如果函数 $f(x)$ 在积分区间内不停地在正负之间振荡,可以使用 绝对收敛判别法,即:
\[\boxed{\text{如果}\int_a^b|f(x)|\,\mathrm{d}x\text{收敛,那么}\int_a^b f(x)\,\mathrm{d}x\text{也收敛.}}\]要注意的是,如果积分 $\int_a^b\vert f(x)\vert\,\mathrm{d}x$ 是发散的,不能证明 $\int_a^b f(x)\,\mathrm{d}x$ 是发散还是收敛。
级数的收敛与发散
考虑级数是反常积分的离散化表示,所以,前面四个反常积分敛散性的判别均可直接应用于无穷级数的敛散性判别。除了与反常积分相对应的四个判别法外,级数还有一些特有的敛散性判别法。
1. 第 $n$ 项判别法
对于收敛级数,部分和的极限必须存在。所以,由数列 $\{a_n\}$ 给出的每一步到最后都要变得很小很小,才能使得级数收敛。数学上表示为:当 $n \to \infty$ 时 $a_n \to 0$。因此有
\[\boxed{\textbf{第 n 项判别法:}\text{若} \lim_{n \to \infty} a_n \ne 0\text{,或极限不存在,则级数} \sum_{n=1}^\infty a_n \text{发散.}}\]注意:第 $n$ 项判别法只能判断级数发散,不能判断级数收敛。
2. 比式判别法
考虑一个新的数列 $\{b_n\}$,定义其为级数 $\sum\limits_{n=1}^\infty a_n$ 相邻两项之比的绝对值,即对每个 $n$ 令
\[b_n = \left|\frac{a_{n+1}}{a_n}\right|\]比式判别法结论:
-
$\lim\limits_{n \to \infty}b_n = L \lt 1$,则级数 $\sum\limits_{n=1}^\infty a_n$ 收敛。
-
$\lim\limits_{n \to \infty}b_n = L \gt 1$,则级数 $\sum\limits_{n=1}^\infty a_n$ 发散。
-
$\lim\limits_{n \to \infty}b_n = 1$ 或极限不存在,则无法判断级数敛散性。
3. 根式判别法
根式判别法也叫 $n$ 次方根判别法,类似于比式判别法,考虑的不是级数 $\sum\limits_{n=1}^\infty a_n$ 相邻项的比,而是第 $n$ 项绝对值的 $n$ 次方根,即新数列 $\{b_n\}$ 为
\[b_n = |a_n|^{\frac{1}{n}}\]根式判别法结论:
-
$\lim\limits_{n \to \infty}b_n = L \lt 1$,则级数 $\sum\limits_{n=1}^\infty a_n$ 收敛。
-
$\lim\limits_{n \to \infty}b_n = L \gt 1$,则级数 $\sum\limits_{n=1}^\infty a_n$ 发散。
-
$\lim\limits_{n \to \infty}b_n = 1$ 或极限不存在,则无法判断级数敛散性。
3. 积分判别法
若对连续递减正函数 $f$ 有 $f(n)=a_n$,则
\[\int_1^\infty f(x)\,\mathrm{d}x \quad 和 \quad \sum_{n=1}^\infty a_n\]同时收敛或同时发散。
4. 交错级数判别法
如果级数 $\sum\limits_{n=1}^\infty a_n$ 各项正负交错出现,称为交错级数。给正项级数的各项乘以 $(-1)^n$ 或 $(-1)^{n+1}$ 就可得到一个交错级数。如:
\[\sum_{n=1}^\infty\frac{(-1)^n}{n^2} \quad 和 \quad \sum_{n=1}^\infty\frac{(-1)^n}{n}\]使用绝对收敛判别法和 $p$ 判别法可知,第一个级数绝对收敛,第二个级数不是绝对收敛,但证明可知原级数是收敛的。当一个级数收敛而其绝对值形式发散,我们就说该级数条件收敛。
交错级数判别法结论:
若级数 $\sum\limits_{n=1}^\infty a_n$ 是交错级数,当 $\vert a_n \vert$ 递减且 $ \lim\limits_{n \to \infty}\vert a_n \vert = 0$ 时,则级数收敛。
泰勒多项式
泰勒近似定理
若 $f$ 在 $x=a$ 处光滑,则在所有次数为 $N$ 或更低的多项式中,当 $x$ 在 $a$ 附近时,最近似于 $f(x)$ 的是
\[\begin{aligned} P_N(x) &= \sum_{n=0}^N \frac{f^{(n)}(a)}{n!}(x-a)^n \\[2ex] &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f^{(3)}(a)}{3!}(x-a)^3 + \cdots + \frac{f^{(N)}(a)}{N!}(x-a)^N \end{aligned}\]多项式 $P_N$ 为 $f(x)$ 在 $x=a$ 处的 $N$ 阶泰勒多项式。
注意:$0$ 的 $0$ 次幂 (Zero to the power of zero)是数学中的不定式之一。在多项式中,一般定义 $0^0 = 1$。此外,$0!=1$,$f^{(0)}(x)$ 表示函数 $f(x)$ 的零阶导数,因此 $f^{(0)}(x)=f(x),f^{(1)}(x)=f’(x)$。
$P_N$ 的重要性质是,对所有 $n=0,1,\dots,N$
\[P_N^{(n)}(a) = f^{(n)}(a)\]即多项式 $P_N(x)$ 的 $n$ 阶导数在 $x=a$ 处等于其近似的函数 $f$ 的 $n$ 阶导数 $f^{(n)}(x)$,多项式 $P_N$ 提取了函数 $f$ 在 $x=a$ 处直到 $N$ 阶导数的所有信息,并且 $P_N$ 所有更高阶的导数处处为 $0$。
因为 $P_N$ 是函数 $f(x)$ 的近似,那么它们之间存在一个误差项 $R_N$
\[R_N(x) = f(x) - P_N(x)\]$R_N(x)$ 被称为 $N$ 阶误差项或 $N$ 阶余项。
泰勒定理
关于 $x=a$ 的 $N$ 阶余项
\[R_N(x) = \frac{f^{(N+1)}(c)}{(N+1)!}(x-a)^{(N+1)}\]其中 $c$ 是介于 $x$ 与 $a$ 之间的一个数。
幂级数和泰勒级数
$x=a$ 处的幂级数
\[\sum_{n=0}^\infty a_n(x-a)^n = a_0 + a_1(x-a) + a_2(x-a)^2 +a_3(x-a)^3 + \cdots\]$x=0$ 处的幂级数
\[\sum_{n=0}^\infty a_nx^n = a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots\]泰勒级数
$f$ 在 $x=a$ 处的泰勒级数
\[\sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n\]可以看出,泰勒多项式 $P_N(x)$ 是泰勒级数的 $N$ 项部分和。
麦克劳林级数
$f$ 在 $x=0$ 处的泰勒级数,称为麦克劳林级数
\[\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n\]