三角函数
学用的三角函数值
| 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | |
|---|---|---|---|---|---|
| sin | 0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | 1 |
| cos | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | 0 |
| tan | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | Undefined |
单位圆
在数学中,单位圆 (Unit circle) 是指半径为单位长度的圆,通常为欧几里得平面直角坐标系中圆心为 $(0, 0)$ 、半径为 1 的圆。
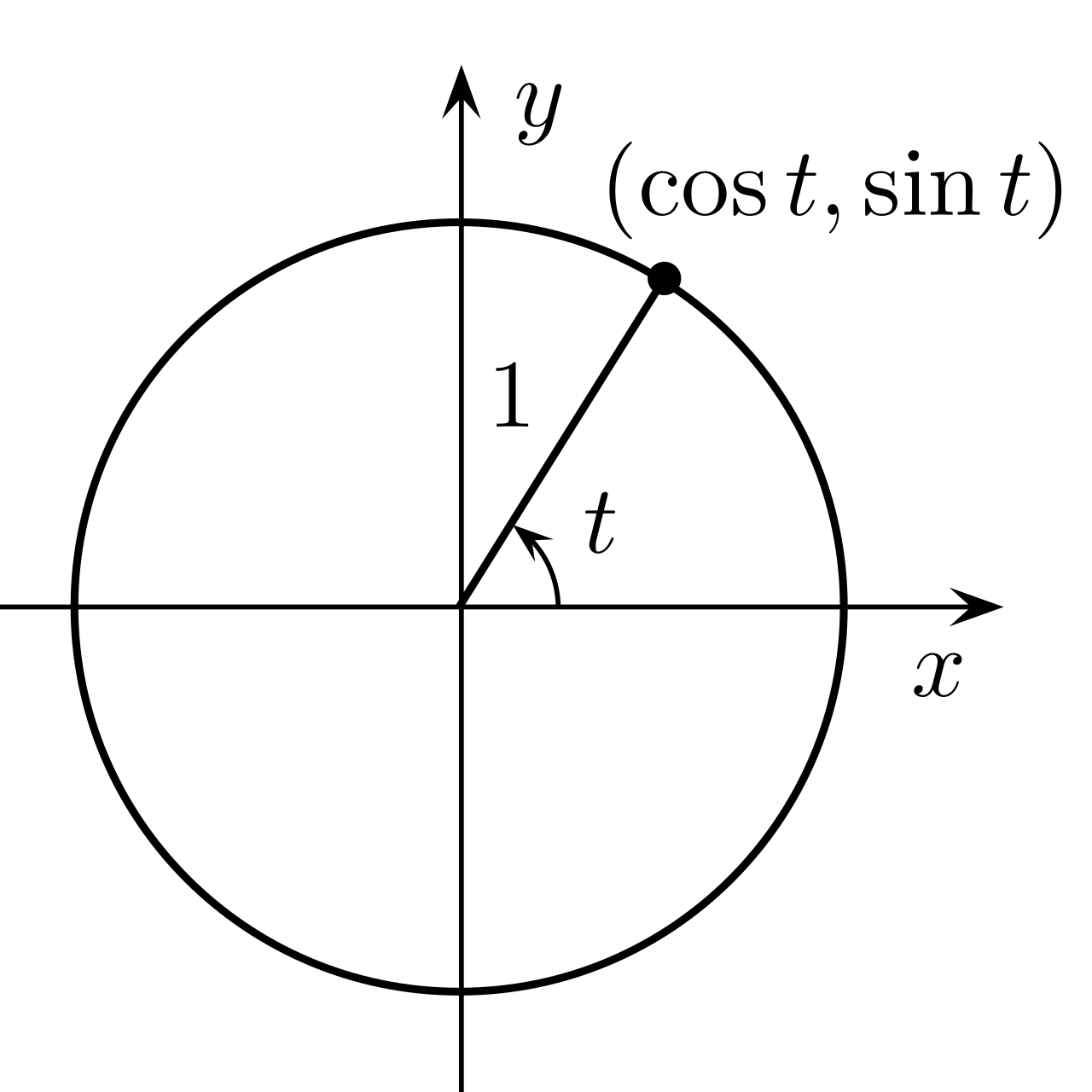

设 $(x, y)$ 是单位圆上的一个点,那么
\[\begin{align*} \cos{t} = \frac{x}{1} = x \\ \sin{t} = \frac{y}{1} = y \end{align*}\]点 $(x, y)$ 可以由 $(\cos{t}, \sin{t})$ 来表示。
单位向量
单位向量是指模等于1的向量。由于是非零向量,单位向量具有确定的方向。
一个非零向量除以它的模,可得所需单位向量。设原来的向量是 $\overrightarrow{AB}$,则与它方向相同的单位向量 $e=\frac{\overrightarrow{AB}}{\vert AB \vert}$;
单位向量的性质:
- 单位向量的长度为1个单位,方向不受限制。
- 起点为原点的单位向量,终点分布在单位圆上,常可设为 $\overrightarrow{a}=(\cos{\alpha}, \cos{\beta})$,反之亦然。
- 如果 $AB$ 为非零向量,那么与 $AB$ 共线的单位向量为 $\pm\frac{\overrightarrow{AB}}{\vert AB \vert}$。
方向导数
方向导数本质上研究的是函数在某点处沿某特定方向上的变化率问题。
极限公式:
\[\begin{align} \left.\frac{\partial{z}}{\partial{\overrightarrow{l}}}\right \vert _{(x_0, y_0)} &= \lim_{t\rightarrow 0} \frac{f({x_0+\Delta x, y_0+\Delta y}) - f(x_0, y_0)}{t} \\[2ex] &= \lim_{t\rightarrow 0} \frac{f({x_0+t\cos\alpha, y_0+t\cos\beta}) - f(x_0, y_0)}{t} \end{align}\]另一方面,方向导数又与偏导数密不可分
\[\left.\frac{\partial{z}}{\partial{\overrightarrow{l}}}\right \vert _{(x_0, y_0)} = \frac{\partial{f}}{\partial{x}}\cos\alpha + \frac{\partial{f}}{\partial{y}}\cos\beta\]梯度
梯度是一个向量,它的每个分量是函数关于该点各自变量的偏导数。数学上,对于一个函数 $f(x_1,x_2,\dots,x_n)$,其梯度表示为:
\[\nabla{f} = \left(\frac{\partial{f}}{\partial{x_1}},\ \frac{\partial{f}}{\partial{x_2}},\ \dots,\ \frac{\partial{f}}{\partial{x_n}}\right)\]