反向传播(Backpropagation)
反向传播是通过计算假设函数与真实值之间的误差值($error = h_\theta(x^{(i)}) - y^{(i)}$),并反向传播这个误差值,最终用于计算参数 $\theta_{ij}$ 的偏导数。支撑这一理论的核心思想是多元复合函数的链式求导,下面通过一个简单的例子进行描述。
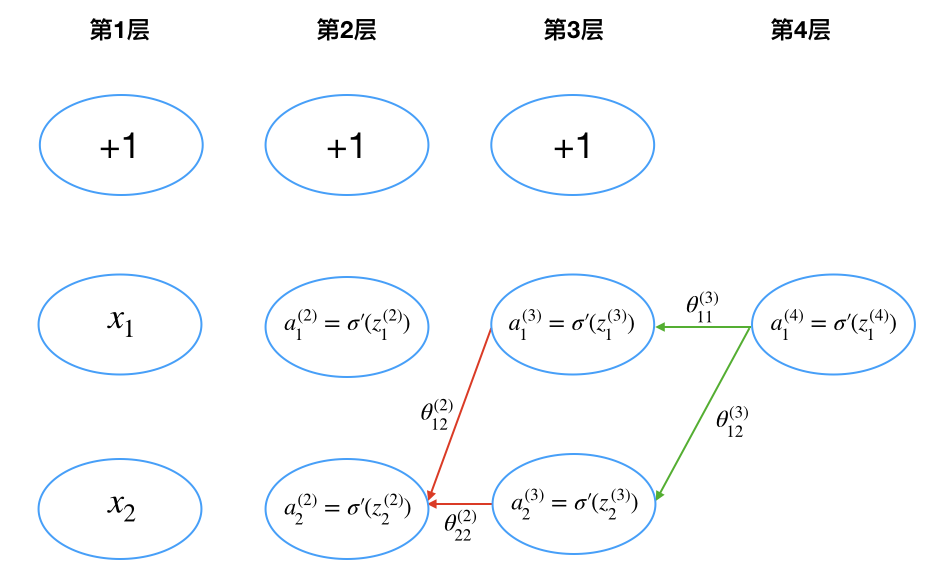
例如,计算代价函数关于 $z^{(2)}_2$ 的偏导数,根据这里的求导结果,可知
\[\begin{aligned} \dfrac{\partial C}{\partial z^{(2)}_2} &= \color{blue}{\dfrac{dC}{a^{(4)}_1}\dfrac{da^{(4)}_1}{dz^{(4)}_1}}\color{green}{\dfrac{\partial z^{(4)}_1}{\partial a^{(3)}_1}\dfrac{da^{(3)}_1}{dz^{(3)}_1}}\color{red}{\dfrac{\partial z^{(3)}_1}{\partial a^{(2)}_2}\dfrac{da^{(2)}_2}{dz^{(2)}_2}} + \color{blue}{\dfrac{dC}{a^{(4)}_1}\dfrac{da^{(4)}_1}{dz^{(4)}_1}}\color{green}{\dfrac{\partial z^{(4)}_1}{\partial a^{(3)}_2}\dfrac{da^{(3)}_2}{dz^{(3)}_2}}\color{red}{\dfrac{\partial z^{(3)}_2}{\partial a^{(2)}_2}\dfrac{da^{(2)}_2}{dz^{(2)}_2}} \\ &= \color{blue}{(a^{(4)}_1 - y)} \cdot \color{green}{\theta^{(3)}_{11} \cdot \sigma'(z^{(3)}_1)} \cdot \color{red}{\theta^{(2)}_{12} \cdot \sigma'(z^{(2)}_2)} + \color{blue}{(a^{(4)}_1 - y)} \cdot \color{green}{\theta^{(3)}_{12} \cdot \sigma'(z^{(3)}_2)} \cdot \color{red}{\theta^{(2)}_{22} \cdot \sigma'(z^{(2)}_2)} \end{aligned}\]其中
\[\begin{aligned} \color{blue}{\delta^{(4)}_1} &= a^{(4)}_1 - y \\ \color{green}{\delta^{(3)}_1} &= \color{blue}{\delta^{(4)}_1} \cdot \color{green}{\theta^{(3)}_{11} \cdot \sigma'(z^{(3)}_1)} \\ \color{green}{\delta^{(3)}_2} &= \color{blue}{\delta^{(4)}_1} \cdot \color{green}{\theta^{(3)}_{12} \cdot \sigma'(z^{(3)}_2)} \\ \color{red}{\delta^{(2)}_2} &= \color{green}{\delta^{(3)}_1} \cdot \color{red}{\theta^{(2)}_{12} \cdot \sigma'(z^{(2)}_2)} + \color{green}{\delta^{(3)}_2} \cdot \color{red}{\theta^{(2)}_{22} \cdot \sigma'(z^{(2)}_2)} \\ &= \color{green}{\begin{bmatrix} \delta^{(3)}_1 \\ \delta^{(3)}_2 \end{bmatrix}} \color{red}{\begin{bmatrix} \theta^{(2)}_{12} \\ \theta^{(2)}_{22} \end{bmatrix} \cdot \sigma'(z^{(2)}_2)} \\ &= (\color{red}{(\theta^{(2)})^T} \color{green}{\delta^{(3)})} \cdot \color{red}{\sigma'(z^{(2)}_2)} \end{aligned}\]上面代价函数关于 $z^{(2)}_2$ 的偏导数即为:
\[\dfrac{\partial C}{\partial z^{(2)}_2} = \delta^{(2)}_2\]根据上面的推论我们定义:
\[\dfrac{\partial C}{\partial z^{(l)}_j} = \delta^{(l)}_j = ((\theta^{(l)})^T \delta^{(l+1)}) \cdot \sigma'(z^{(l)}_j)\]向量化形式:
\[\dfrac{\partial C}{\partial z^{(l)}} = \delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)}) \odot \sigma'(z^{(l)})\]最终,我们可以通过错误量 $\delta$ 很方便的计算任意参数 $\theta$ 的偏导数 $\dfrac{\partial C}{\partial \theta^{(l)}_{ij}}$
\[\begin{aligned} \dfrac{\partial C}{\partial \theta^{(l)}_{ij}} &= \dfrac{\partial C}{\partial z^{(l+1)}_i}\dfrac{\partial z^{(l+1)}_i}{\partial \theta^{(l)}_{ij}} \\ &= \delta^{(l+1)}_i \cdot a^{(l)}_j \end{aligned}\]